Etudier la dérivabilité, calculer la dérivée et dresser le tableau de variation d'une fonction avec racine carrée
-
Ssil2b dernière édition par Hind
bonjour, est ce que quelqu'un pourrait m'aider pour cet exercice.
soit f(x)=x racine carée de (x-x²)
1)montrer que f est dérivable sur ]0;1[ et calculer f'(x)
2)étudier le signe de f' et dresser le tableau de variations de f
-
déterminer lim quand h tend vers o de f(h)-f(0)/h-o
f est elle dérivable en 0? donner l'équation de la tangente à la courbe c au point d'abscisse o. -
montrer que pour tout h de ]-1;0[:[f(1+h)-f(1)]/h = -(1+h)racine carrée de [-1-(1/h)]. f est elle dérivable en 1? donner l'équation de la tangente à c au point d'abscisse 1.
-
tracer la courbe
-
-
Ssil2b dernière édition par
comment doit on faire pour montrer que f est dérivable sur ]0;1[
-
Aasumah dernière édition par
le racine caree est derivable sur son domainde de definition a l exeption du point ou il est null c est a dire que f est derivable sur ]0;1[.
-
Ssil2b dernière édition par
ok, et à la question 3) l'équation de la tangente est bien y=0 ?
-
Aasumah dernière édition par
oui, puis ce que la limite demande donne 0
alors l'equation de la tengente est y=0
-
Ssil2b dernière édition par
comment fait on pour la 4)
-
Aasumah dernière édition par
on f(1) = 0
alors on va simplifier f(h+1)/h=
[ (1+h)foi racine carre de [(1+h)-(1+h)^2] ]/hon va faire entre h dans le racine, on h < 0 alors on va ajoute un - et ca deviendra:
-(1+h) * racine de [((h+1) - (h+1) ^2)/ h^2]
on simplifiant tu trouvera -(1+h) * racine de [-(h+1)/h]
cet ce qu on cherche
-
Ssil2b dernière édition par
on fait rentrer le h du dénominateur dans la racine, mais on peu pas l'enlever du dénominateur comme ca
-
Aasumah dernière édition par
−(1+h)×(1+h)−(1+h)2/h2-(1+h) \times \sqrt(1+h) - (1+h)^2 / h^2−(1+h)×(1+h)−(1+h)2/h2
−(1+h)×(1+h)(1−h−1)/h2-(1+h) \times \sqrt(1+h)(1-h-1) / h^2−(1+h)×(1+h)(1−h−1)/h2
−(1+h)×(1+h)×−1/h-(1+h) \times \sqrt(1+h) \times -1 / h−(1+h)×(1+h)×−1/h
−(1+h)×(−1−h)/h-(1+h) \times \sqrt(-1-h) / h−(1+h)×(−1−h)/h
−(1+h)×(−1−h)/h-(1+h) \times \sqrt(-1-h) / h−(1+h)×(−1−h)/h
-
Ssil2b dernière édition par
je ne comprend pas trop le calcul que tu m'a fais quand tu fais rentrer le h du dénominateur dans la racine. en plus il devient h² ???
-
Aasumah dernière édition par
puis ce que h est negatif alors on va ajoute un -
et pour le h qui va rentrer sa devient h² puis va simplifier avec (1-h-1)
-
Ssil2b dernière édition par
c'est ok, j'ai trouvé merci. euh, par contre, comment on fait pour dire que f est dérivable en o (question 3) et en 1 (question 4)?
-
Zorro dernière édition par

Bonjour,
Pour démontrer qu'une fonction est dérivable en x0x_0x0 , on utilise la définition.
On cherche la limite de ....... en ....
-
Ssil2b dernière édition par
question 4) f est elle dérivable en 1? il faut faire limite de -1(1+h)Racine(-1-(1/h)) quand h tend vers 1 et trouver une limite finie??
-
Ssil2b dernière édition par
- j'ai essayé de faire la limite de -(1+h)racine(-1-(1/h)) quand h tend vers 1 mais c'est impossible car on a -2*racin(-2)?? elle n'est pas dérivable en 1 alors??
-
IIron dernière édition par
Bonjour sil2b,
Par définition, f est dérivable en x0x_0x0 ssi :
lim { [f(x[f(x[f(x_0+h)−f(x0+h)-f(x_0+h)−f(x0)]/h } existe et est finie
h→0quand on utilise cette définition, h tend vers 0 et non pas vers x0x_0x0.
Ici x0x_0x0 = 1 bien sûr et sers toi de l'égalité qui vient d'être démontrée.
Que ce soit dans ce post ou l'autre un peu du même genre, tu bloques sur le
cours de 1ère! Je ne peux que te conseiller de combler vite ces lacunes, revois la dérivabilité, les études de fonction, ...
-
Ssil2b dernière édition par
ok, iron. je remplace h par 0 dans -(1+h)racine(-1-(1/h))
-(1+0)racine((-h-1)/h)=-racine(-1/0). 1/o est une forme semi indéterminer. la, h tend vers o+, la limite de -(1+h)racine(-1-(1/h)) est
-infini donc f n'est pas dérivable en 1. c'est plutot comme ca ?
-
IIron dernière édition par
En fait, ici h = x−1 et quand x tend vers 1−1^-1− alors h tend vers 0−0^-0−
(h ne peut pas être strictement positif, l'intérieur de la racine serait négatif)
lim [f(1+h)-f(1)]/h = lim {-(1+h) √[-1-(1/h)] } = -∞
h → 0−0^-0−car c'est de la forme {-1 × √[-1-(-∞)]} soit {-1 × +∞}
f n'est donc pas dérivable en 1.
La tangente à Cf en 1 est donc . . .
Tu peux te référer à ce pdf de Zauctore
-
Ssil2b dernière édition par
l'équation de la tangente au point d'abscisse 1 est : y=0
-
IIron dernière édition par
Non,
La tangente au point de coordonnées (1;0) est verticale déquation x = 1
-
Ssil2b dernière édition par
il y a bien 2 tangentes, une en 0 et une en 1. les 2 ont une équation : y=0 d'après les calculs??
-
IIron dernière édition par
Non, f n'est pas dérivable en 1. La tangente au point de coordonnées (1;0) est verticale d'équation x = 1
-
Ssil2b dernière édition par
au final, je ne sais pas trop comment tracer les tangentes. il y en a bien 2?
-
IIron dernière édition par
Oui, il y en a 2
à l'origine O, la tangente est horizontale, elle correspond à l'axe de abscisse d'équation y=0
Au point de coordonnées (1;0), la tangente est verticale d'équation x = 1
-
IIron dernière édition par
Tu as trouvé la limite de [f(h)-f(0)]/(h-o) quand h tend vers 0 ?
Qu'as-tu répondu à la question 3) ? Est-elle dérivable en 0 ?
-
IIron dernière édition par
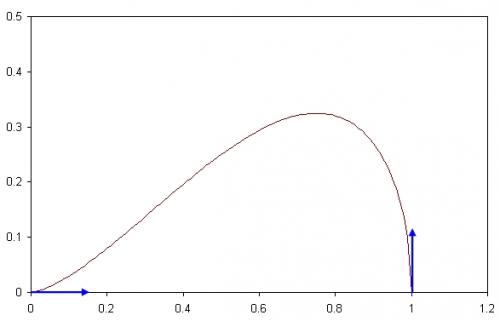
Tu pourrais également tracer la tangente horizontale au point d'abscisse qui annule la dérivée (le sommet de la courbe)
-
Vvaccin dernière édition par
bonjour
sauf erreur de calcul lorsqu'on élève au carré on trouve:
y²=x-x²
ce qui peut s'écrire
x²+y²-x=0
ou, encore
(x-1/2)² +y²=1/4
on peut reconnaître l'équation d'un cercle de centre(1/2,0) et de rayon 1/2.bonne journée
-
Ssil2b dernière édition par
question 3) lim f(h)-f(0)/(h-0) quand h tend vers 0 = 0. la limite est finie donc f dérivable en 0. tangente au point 0 : y=0
- lim -(1+h) racine(-1-1/h) quand h tend vers 0 = -infini. la limite n'est pas finie donc f n'est pas dérivable en 1. tangente en 1 : y=0
-
Vvaccin dernière édition par
bonjour
j'aimerais vous convaincre que les équations de tangentes que vous donnez sont fausses.
en réalité il s'agit de x=0 en 0 et de x=1 pour x=1@+
-
Ssil2b dernière édition par
comment sait on lorsqu'une tangente est horizontale, verticale.
-
IIron dernière édition par
La tangente est horizontale pour les points dont l'abscisse annule la dérivée : Pour ta fonction, f'(3/4) = 0, au point de coordonnées (3/4;f(3/4)) Cf admet une tangente horizontale.
Si la limite de [f(x[f(x[f(x_0+h)−f(x0+h)-f(x_0+h)−f(x0)]/h existe et est infinie quand h tend vers 0, on admet qu’il existe une tangente de pente infinie donc verticale, d’équation x = x0x_0x0
C’est le cas ici pour x = 1, la tangente au point de coordonnées (1;0) est verticale d’équation x = 1
Le taux de variation au voisinage de 0 tend vers 0. Vaccin suggère une tangente d’équation x = 0. Je lui fais confiance mais je n’ai pas compris.
-
Vvaccin dernière édition par
bonsoir
la dérivée de √(x-x²) est (-2x+1)/2√(x-x²).
lorsque x tend vers o le numérateur vaut 1 et le dénominateur tend vers 0
le quotient tend vers l'infini d'où la tangente verticale.
lorsque x tend vers 1 le num vaut -1 et le dénom 0
etc...
c'est clair quand on a vu qu'il s'agit d'un demi-cercle.
bonne soirée
-
IIron dernière édition par
Bonsoir vaccin,
La fonction est : f(x)=xx−x2f(x)= x \sqrt{x-x^{2}}f(x)=xx−x2
Lorsque l'on calcule le taux de variation en 0, on obtient x−x2\sqrt{x-x^{2}}x−x2 il me semble. Sa limite quand x tend vers 0 est égale à 0, non ?
-
Vvaccin dernière édition par
bonjour
mes excuses j'ai lu f(x)=√(x-x²)
je vais acheter des lunettes et revoir...
@+
-
IIron dernière édition par
Bonjour Vaccin,
Aucun souci. Il faut dire aussi que sans l’utilisation des caractères mathématiques, l’énoncé de sil2b n’est pas très clair.
Bonne journée et à +
-
Ssil2b dernière édition par
bonjour, au final les tangentes sont horizontales, verticales?
d'autre part, comment fait on pour utiliser l'écriture latex?
-
IIron dernière édition par
Iron
Oui, il y en a 2à l'origine O, la tangente est horizontale, elle correspond à l'axe de abscisse d'équation y=0
Au point de coordonnées (1;0), la tangente est verticale d'équation x = 1
Sous le cadre de saisie, il y a
Ajoute une formule mathématique - Editeur LaTeXSans aller jusqu'au latex, tu peux utiliser les boutons √ à conditions d'utiliser les () à bon escient.
-
Vvaccin dernière édition par
http://www.mathcurve.com/courbes2d/piriforme/piriforme.shtml
si je copie bien et si le lien fonctionne comme prévu il y a ici le dessin d'une " quartique piriforme " qui ressemble bigrement à la moitié de la courbe proposée...
bonne journée
-
Ssil2b dernière édition par
j'ai demandé à quelqu'un pour les tangentes, on m'a dit qu'elles sont toutes les 2 horizontales.??? or, d'après toi en o elle est horizontale et en 1 elle est verticale
-
IIron dernière édition par
vaccin
http://www.mathcurve.com/courbes2d/piriforme/piriforme.shtml
si je copie bien et si le lien fonctionne comme prévu il y a ici le dessin d'une " quartique piriforme " qui ressemble bigrement à la moitié de la courbe proposée...
Intéressant ce site et effectivement c'est tout à fait ça, une "quartique piriforme" avec a=b=1, une "larme".