Déterminer en combien de temps se remplit le lavoir
-
Sstephbleu dernière édition par Hind
Pour remplir le lavoir municipal, l'employé de mairie dispose se 3 robinets différents. Le débit de chaque robinet est constant, que les autres soient ouverts ou non. Lorsque l'employé ouvre à la fois le premier et le deuxième robinets, le troixieme etant ferme, le lavoir se remplit en 1 heure et 10 minutes. Lorsqu'il ouvre à la fois le premier et le troixieme robinets, le deuxieme etant ferme, le lavoir se remplit en 50 minutes. Lorsqu'il ouvre à la fois le deuxieme et le troixieme robinets, le premier etant fermé, le lavoir se remplit en 56 minutes. S'il ouvre à la fois les trois robinets, en combien de temps se remplit le lavoir ?
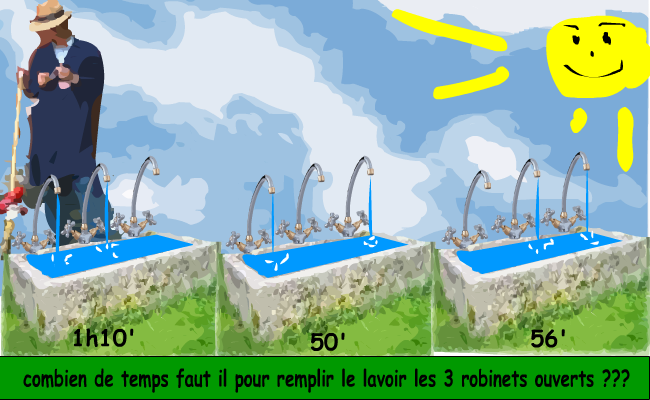
-
Fflight dernière édition par
coucou!
soient dm1/dt le débit du 1 ier robinet en kg par unité de temps
dm2/dt le debit du 2 ieme robinet
et dm3/dt "............" du 3 ieme robinetsoit Q la valeur massique maximale du bassin apres remplissage en kg
si 1 et 3 sont ouverts et 2 et fermé, alors;
alors le temps de remplissage avec 1 et 3 est
T(1/2)=Q/(dm1/dt+dm2/dt) avec T(1/2)=4/3 en heuresi 1 et 3 sont ouverts et 2 est fermé , alors;
T(1/3)=Q/(dm1/dt+dm3/dt) avec T(1/2)=5/6 en heure
plus simplement posons dm1/dt=A, dm2/dt =B et dm3/dt=C
on a
A+B=Q/T(1,2)
A+C=Q/T(2,3)
B+C=Q/T(1,3)si 2 et 3 sont ouverts et 1 est fermé, alors;
T(2/3)=Q/(dm2/dt+dm3/dt) avec T(2/3)=56/60=14/15 en heure
on a donc un beau systeme d'équation en dm1/dt , dm2/dt et dm3/dt.
on en tire par exemple B=Q/2.(1/T(1,2)-1/T(2,3)+1/T(1,3))
on fait pareil pour A et C .
puis pour connaitre le temps global de remplissage du reservoir avec tout les robinets
il suffit d'écrire que Tg=Q/(A+B+C)
A+
-
Fflight dernière édition par
... j'allais oublier , Q s'eliminera en effectuant le quotient Tg=Q/(A+B+C) car A , B et C sont donnés en fonction de Q
a+
-
Jj-gadget dernière édition par
Je suis de retour ! Bon, pour ce problème, il y a plus simple (je pense):
convertissons tout en minutes et prenons le PPCM pour que ça tombe juste.
PPCM(70;50;56)=9800
A et B : 140 lav. en 9800 min
A et C : 196 lav. en 9800 min
B et C : 175 lav. en 9800 min
Tout ensemble: 2A+2B+2C : 511 lavoirs en 9800 minutes soit
1 lavoir par 19,178 minutes. Mais A+B+C c'est 2 fois moins de robinets donc les 3 remplissent le lavoir en environ 38 min 21 s . Voilà !
-
j-gadget ! les énigmes sont de retour ... voilà !
-
Jj-gadget dernière édition par
Content de voir que je n'ai pas été oublié ! Prochaine énigme tout de suite . Voilà !