Trouver le meilleur encadrement possible d'une fonction sur un intervalle

Bonjour , j'ai un devoir à rendre pour mardi.
Mais j'ai un énorme problème , la prof nous a donné un exercice sur les encadrements alors qu'on a jamais fait de cours...
Pourriez-vous m'aider ??

1/ a/ Quel est le sens de variation de f sur [-3,0] FACILE
b/ En déduire le meilleur encadrement possible de f(x) sur [-3;0]

2/b/ En déduire le meilleur encadrement possible de f(x) sur [0;2]

3/b/ On sait que x est un réel de [2;4] et que -2 ≤ f(x) ≤ 1. Donner le meilleur encadrement possible de x

4/Sachant que -3 ≤ x ≤ 2 , donner le meilleur encadrement possible de f(x).

Je suis vraiment perdu car je ne connais pas du tout cela! Merci de votre aide
Desole pour la qualité de l'image :s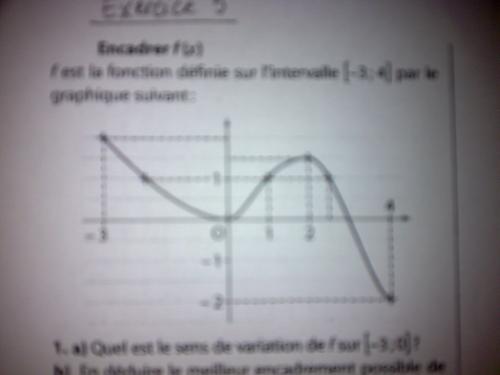

$fichier math$

**** Edit Zorro : ajout d'espaces pour que l'image s'affiche et changement d'inférieur ou égal en ≤ ****

Bonjour,

Encadrer un nombre c'est dire que ce nombre est compris entre ... et ----

Donc encadrer f(x) c'est trouver les nombres tels que ??? ≤ f(x) ≤ ???????

Donc par exemple pour le 1b/ -3 < f(x) < 0 ??

sur [-3;0] f est ....... et f(-3) = ? de plus f(0) = ?? donc ????? ≤ f(x) ≤ ??

Tu confonds x et f(x) .....

Dans la phrase """sur [-3;0] f est ......."""" c'est x qui appartient à [-3 ; 0]

soit -3 ≤ x ≤ 0

f(x) c'est les y.
Donc sur [-3;0] f est decroissante et f(-3) = 2 et f(0) = 0 donc 2 ≤ f(x) ≤ 0 ??

Non ?

oui. C'est juste !

Tu essayes les autres !