exercice sur les fonctions avec tangente, dérivée, limites
-
Cchiper dernière édition par
J'ai un devoir maison a rendre pour la fin de la semaine malheureusement j'ai du mal le faire. Pouvez vous, s'il vous plait, m'aider à comprendre et m'aider à faire celui ci. Merci d'avance.
Voici l'énoncé :
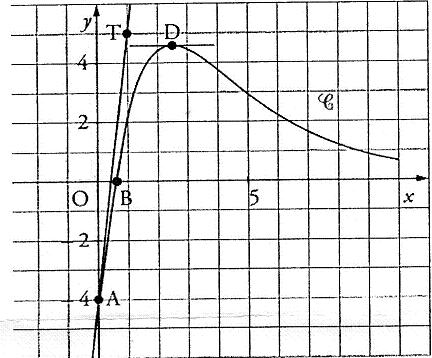
La courbe C ci-contre est la représentation graphique dans un repère orthonormal d'une fonction f définie et dérivable sur R.
Les points A (0 ; -4), B (0.5 ; 0) et D (2.5 ; 4.6) appartiennent à C. La courbe C admet en D une tangente parallèle à l'axe des abscisses. La tangente à C en A passe par T (1 ; 5)
- par lecture graphique en justifiant :
- donner les valeurs de f(0), f'(0) et f'(2.5)
- donner les solutions dans [0 ; 10] de l'inéquation f(x)<0
- donner les solutions dans [0 ; 10] de l'inéquation f'(x)<0
- donner une équation de la tangente à C en A
- donner une équation de la tangente à C en D
- Soit g la fonction définie par g(x)=√f(x). Répondre aux questions suivantes en justifiant.
- donner l'ensemble de définition de g
- donner les tableau de variation de g
-trouver
lim g(x)
x→+∞
Je sais que f'(a) est la pente de la tangente à la courbe au point d'abscisse a.
f'(x)>0 signifie que la courbe est croissante au point d'abscisse x.
L'équation de la tangente au point d'abscisse a est de la forme y=f'(a)(x-a)+f(a) est-ce bon pour l'instant ? pouvez vous m'aider pour la suite svp merci !

-
Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
Le 1) est à réaliser par lecture graphique à justifier.
-
Cchiper dernière édition par
j'ai résolu le 1 mais le tableau de variation et la limite de g me pose problème... peux-tu m'aider s'il te plait

-
Bonjour,
Quelles sont les variations de f pour x variant sur l'intervalle [0,5 ; +∞ [ ?
Quelle est la limite de f(x) quand x tend vers +∞ ?
-
Cchiper dernière édition par
Sur [0.5 ; 2.5[ f(x) est croissante et sur [2.5 ; +∞[ f(x) est décroissante
et pour la limite je ne sais pas ...
-
N'ayant pas la limite de f(x), quand x tend vers +∞, on ne peut en déduire la limite de g(x) en + ∞.
On peut faire des hypothèses.
si la limite de f(x) en + ∞ et 0+, la limite de g(x) en +∞ est 0+.