Tronc d'une pyramide

Bonjour tout le monde
J'ai essayé de résoudre cet exercice depuis quelques heures déjà, en vain .
Voici l'énoncé:
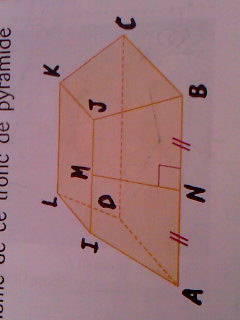
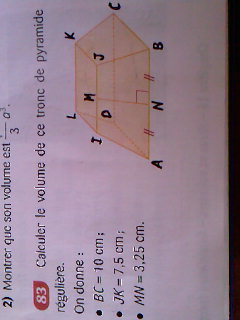
Calculer le volume de ce tronc de pyramide régulière,
On donne:

AB= 10 cm
JK= 7,5 cm
MN= 3,25 cm

Merci de bien vouloir m'éclairer, je suis assez perdue à vrai dire .

$fichier math$

Bonjour,

Quelle formule connais-tu pour le volume d'un tronc de pyramide ?

Je n'en connais pas, et même si j'en connaissais une, j'aurai je pense, besoin de connaître la hauteur du tronc ou bien celle de la pyramide tronquée .
Comment procèderiez-vous ?

Bonjour,
ta pyramide étant qualifiée de "régulière", je suppose que ses bases (ABCD et IJKL) sont des carrés.
Peux-tu confirmer ?

Je suppose que la pyramide est régulière ?

Si O est le sommet de la pyramide, calcule la distance ON puis la hauteur de la pyramide.

Comment calcule t-on le volume d'une pyramide ?

La pyramide étant régulière ses bases sont des carrés .
J'ai essayé de calculer ON et la hauteur, mais je ne vois pas comment faire, j'ai essayé d'employer les théorèmes de Thalès et Pythagore, en vain .
Le calcul du volume d'une pyramide est le suivant:
1/3 x B x h

Pour calculer ON, utilise la propriété de Thalès.

Indique tes calculs.

Oui mais pour appliquer Thalès, il faudrait que je connaisse la longueur OM, or on ne la connait pas !

Vu que tu connais MN, calcule OM, puis tu en déduiras ON.

Je sais pas comment faire pour calculer OM en utilisant Thalès . Je suis sérieuse, aidez moi je comprends pas trop comment procéder

Tu écris les rapports :
OM/ON = OJ/OB = MJ/NB

Remplace les termes que tu connais en posant OM = x.

Je en connais ni OM/ON, ni OJ/OB, seulement MJ/NB= 3,25/5

OM = x et ON = OM + MN avec MN = 3,25
Soit ON = ....

ON=x+3,25

Oui,

Ecris les rapports et calcule x.

OM/ON=MJ/NB

x/x+3,25= 3,25/5, après je ne sais pas

C'est :
x/(x+3,25)= 3,75/5

Comment tu résous : x/4 = 6/5 ?

C'est 3,25/5 .

Ben x= (6 x 4 ) / 5

Applique le même raisonnement.

Pourquoi 3,25/5 ?? car JK = 7,5

Ah oui désolée c'est bien 3,75/5 !

et bien :
x= 3,75 fois (x+3,25) / 5

Donc de là je fais
x= 3,75 + 12,1875 /5
x= 3,75/5 + 12,1875/ 5
en multipliant des deux côtés par 5 pour faire disparaître les fractions on obtient :

5x= 3,75x+ 12,1875
1,25x = 12,1875
x = 12,1875/1,25
x=9,75
Donc OM=9,75

x= 3,75 (x+3,25) / 5
Ou
5x = 3,75(x+3,25)

Equation à résoudre.

réalisée ci-dessus

Pour les deux premières lignes, il manque x

Le résultat est juste.
calcule la hauteur.

C'est bon, merci , j'ai trouvé :
On sait donc que OM=9,75
Sachant que ON=OM+MN
Alors ON=9,75+3,25=13

Notons I l'intersection des diagonales de la base carrée .
La longueur NI = 10/2=5
Sachant que le triangle ONI est rectangle en I, le théorème de pythagore s'écrit :
ON²=NI²+IO²
13²=5²+IO²
IO²=144-25
IO=√144
IO=12

On obtient donc la hauteur IO de la pyramide = 12 cm .

À présent il faut calculer le volume de la grande pyramide moins celui de la petite .

V grande pyramide = 1/3 x 100 x 12
V= 1/3 x 1200
V =400 cm³

Soit E l'intersection des diagonales du petit carré supérieur (base de la petite pyramide)

Volume petite pyramide = 1/3 x 56,25 x h (qu'on ne connaît pas )

Tu calcules la hauteur de la petite pyramide à partir de Thalès.

Ah , c'est bon merci je viens de finaliser l'exercice sur feuille !
Merci infiniment de votre précieuse aide tout au long de cet exercice, je vous en suis très reconnaissante .
Au revoir