triangle rectangle en b
-
Ccamomille dernière édition par
j' ai un exercice que j'ai essayé de faire mais je ne parviens pas à le résoudre sur ma feuille je connait ma formule sur thales mais je n' arrive pas à l appliquer
voici l' énoncé:
ABC est un triangle rectangle en B tel que AB = 6 cm, BC= 12 cm
M est un point libre sur [AB] et on pose AM=x
problème: on veut connaître s' il existe des valeurs de x de facon que l' aire du rectangle MPQB soit strictement supérieur à 16 cm²- on désire exprimer en fonction de x l ' aire du rectangle MPQB noté f(x)
1-1 Quelles sont les valeurs possibles de x . En déduire Df
1-2 Explique la démarche de riri fifi et loulou pour exprimer MP,CQ puis PQ en fonction de x
1-3 Déduire des questions précédentes que f(x)=12x-2x²
2)montrer que les solutions du problème ,si elles existent ,sont solutions de l' inéquation f(x)-16>0
3)développer (-2x+8) (x-2). Donner une nouvelle écriture de l' inéquation de la question 2 - Déterminez le signe de (-2x+8) (x-2) en fonction des valeurs de x
voilà tous l 'énoncé de cette exercice avec les images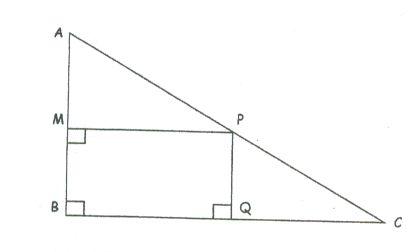
- on désire exprimer en fonction de x l ' aire du rectangle MPQB noté f(x)
-
Zorro dernière édition par

Bonjour,
Et dans tout cela tu n'as vraiment rien trouvé ?
M est un point de [AB] et AM = x donc :
quelle est la plus petite valeur possible pour x ? Et la plus grande ?
-
Ccamomille dernière édition par
non je ne sais pas du tous comment faire car jai des difficultés en math
je nage dans cette matiere la je vais au soutien pour mieux comprendre
si tu peux m aider à résoudre cette exercice sa me permettrait pour une fois d' avoir une bonne note
merci
-
Zorro dernière édition par

x = AM = longueur du segment [AM]
La plus petite valeur de x correspond à la plus petite valeur de AM = longueur du segment [AM]
Et la plus petite valeur de la longueur du segment [AM] c'est quand M est où ?
La plus grande valeur de x correspond à la plus grande valeur de AM = longueur du segment [AM]
Et la plus grande valeur de la longueur du segment [AM] c'est quand M est où ?
Et puis la phrase "je suis nul(le) en maths" c'est une excuse qui ne marche pas toujours. En maths, pour progresser, il faut réfléchir et ne pas croire que les solutions viennent toutes roties sans rien réflexion !
-
Ccamomille dernière édition par
oui je suis tout à fait d accord avec toi mais c est pas des conneries que je te dit j ai que 5 en moyenne en math donc voilà c est pour sa que je ne comprend pas je vais repondre a ta question que tu pose et dit moi si c est sa sinon corrige moi
la plus petite valeur de M est le milieu du [AB] donc 3 cm
et la plus grande valeur du [AB] est 6 cm
-
Zorro dernière édition par

Et pourquoi M devrait être compris entre A et le milieu de [AB] ?
M pourrait bien être être confondu avec A, non ? et dans ce cas AM = .... ?
Et la plus grande valeur de la longueur du segment [AM] est 6 cm , quand M est confondu avec B (c'est juste mais mal justifié).
-
Ccamomille dernière édition par
AM=6cm ?
-
Zorro dernière édition par

Pas vraiment.
M est un point de [AB]
La plus petite valeur possible de la longueur du segment [AM] c'est quand M est confondu avec A , alors AM = AA = 0
La plus grande valeur possible de la longueur du segment [AM] c'est quand M est confondu avec B , alors AM = AB = 6
Tu comprends ?
-
Ccamomille dernière édition par
oui la j ai compris
donc apres il faut faire quoi,
-
Zorro dernière édition par

Avec Pythagore et Thalès, essaye de trouver MP , CQ , PQ
-
Ccamomille dernière édition par
ok j 'essaye de trouver sa je donnerais ma solution
-
Zorro dernière édition par

ça te donnerait la solution
-
Ccamomille dernière édition par
il faut appliquer le theorème de thales c est sa?
MP=BQ
CQ=MP
PQ=MB