Résoudre des équations trigonométriques

[zari]

Bonjour,je dois résoudre cos2x= -1/2 sur I=]-pi;pi]
Donc j'ai fais cos2x=-$pi$/3 <=>2x=-$pi$/3+2 k $pi$<=>x=-$pi$/6 + 2 k $pi$ ou 2x=$pi$/3 + k $pi$ <=> x = $pi$/6 + 2 k $pi$
-$pi$/6 et $pi$/6 appartiennent à ]-$pi$;$pi$] donc S= {-$pi$/6;$pi$/6}
Est ce que c'est juste , merci d'avance .

[Iron]

Bonsoir zari

2×($pi$/6) = $pi$/3 et cos ($pi$/3) ≠ -(1/2) donc c'est faux

Pose X = 2x

cos2x = -(1/2) devient cosX = -(1/2)

Tu en déduis la/les valeur(s) de X puis celle(s) de x

[zari]

Donc pour X c'est -$pi$/6 et $pi$/6 ?

[Iron]

Non,

cos ($pi$/6) = √3/2 et non pas -1/2

utilise le cercle trigonométrique pour trouver les angles de cos -1/2

[zari]

Ben on a -$pi$-3 + 2 k $pi$ et $pi$/3 + 2 k $pi$

[Iron]

C'est la réponse pour X ou x que tu donnes ?

[zari]

pour X

[Iron]

Non

Sur le cercle trigo, les angles de cosinus -1/2 sont les angles +/- 2$pi$/3

Vérifie de ton coté

[zari]

sur le cercle trigo moi j'ai 7$pi$/3 et -$pi$/3

[Iron]

Regarde ICI le cercle trigo posté par Zorro

J'ai des soucis internet ... si je disparais tu comprendras

(Il y a tout sur ce forum !

[zari]

Non moi je suis pas d'accord avec sinus 1/2 ce sont les valeurs en vert sur le cercle trigo

[Iron]

L'axe des cosinus est l'axe horizontal

[Iron]

Bonjour,

Bon, j'ai un peu plus de temps, on reprend doucement :

On veut résoudre cos (2x) = -(1/2) sur I = ]-$pi$;$pi$]

On pose X = 2x

cos (2x) = -(1/2) devient cos X = -(1/2)

On utilise le cercle trigo, l'axe des cosinus est l'axe horizontal :

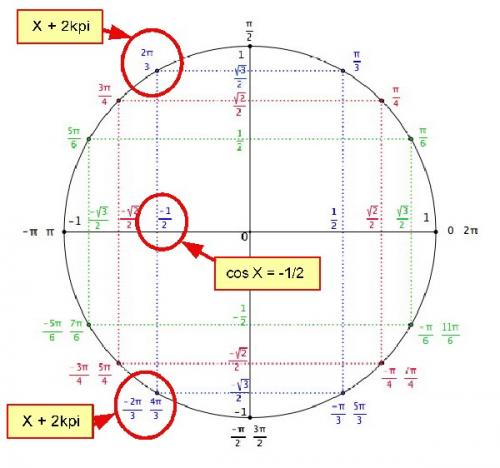
ça nous donne :

| X = 2$pi$/3 + 2k$pi$
| ou
| X = -2$pi$/3 + 2k$pi$

On a posé X = 2x d'où x = X/2

En conclusion :

| x = $pi$/3 + k$pi$
| ou
| x = -$pi$/3 + k$pi$

avec k ∈ $mathbbZ$

Tu as remarqué, il n'y a plus le "2" devant k$pi$.

Comme on veut que les solutions soient dans I = ]-$pi$;$pi$], les solutions sont au nombre de 4 (elles correspondent aux 4 points bleus du cercle trigo) : $pi$/3 -$pi$/3 2$pi$/3 et -2$pi$/3

Exceptionnellement, une solution toute faite car je ne serai pas là ce we. Dis-nous si tu as bien compris la méthode.

[zari]

D'accord merci beaucoup en fait l'erreur que j'ai fait c'est que j'ai confondu cosinus et sinus .
Merci beaucoup de ton aide .