Comment établir les arbres de probabilité
-
MMiYo28 dernière édition par Hind
Bonjour,
J'aurais besoin d'aide pour cet exercice.
Suite à une panne technique, un distributeur de boissons ne tient aucun compte de la commande faite par le client. Cette machine distribue soit un expresso, soit du chocolat, soit du thé en suivant une programmation érronée. Chaque boisson peut etre sucrée ou non .
- La probabilité d'obtenir un expresso est 1/2 .
- La probabilité d'obtenir un thé sucré est 2/9 .
- Si l'on obtient un expresso, la probabilité qu'il soit sucré est 5/9 .
- Si l'on obtient un chocolat, la probabilité qu'il soit sucré est 1/3 .
- La probabilité d'obtenir une boisson sucrée est 5/9 .
On pourra considérer les évènements suivants :
- T: '' On a obtenu un thé ".
- E: '' On a obtenu un expresso ''.
- C:'' on a obtenu un chocolat'' .
- S:'' La boisson obtenue est sucrée ".
- Construire un arbre probabiliste modélisant la situation.
- Calculer la probabilité d'obtenir un expresso sucré.
- Démontrer que la probabilité d'obtenir un chocolat sucré est 1/18 .
- En déduire la probabilité d'obtenir un chocolat .
- Une personne obtient une boisson sucrée. Quelle est la probabilité que cette boisson soit du thé ?
Proposition :
Je ne sais pas comment réaliser les arbres sur ce site. Je traduis en probabilités .
Cependant je n'ai pas pu completer p( T) et p (E)P (E) = 1/2
Je peut déduire que p( T) et p (C) = 0.5 / 2
P (S sachant T ) = 2/9
P (S sachant E ) = 5/9
P (S sachant C ) = 1/3On peut déduire P ( S barre sachant T) = 7/9
P ( S barre sachant E ) = 4/9
P ( S barre sachant C) = 2/3-
P (E inter S) = P (E) * P (S sachanrt E) = (1/2) * (5/9) = (5/18).
-
Je ne sais pas s'il faut appliquer la formule des probabilités totales .
-
Bonsoir,
On ne peux pas déduire que p(T) = p(C) = 1/4.
Cherche en premier la probabilité d'obtenir un expresso sucré.
-
Zorro dernière édition par

Bonjour,
Commençons par traduire l'énoncé :
-
La probabilité d'obtenir un expresso est 1/2 ; donc P(E) = 1/2
-
La probabilité d'obtenir un thé sucré est 2/9 ; donc P(T ∩ S) = 2/9
-
Si l'on obtient un expresso, la probabilité qu'il soit sucré est 5/9 ; donc PEP_EPE(S) = 5/9
-
Si l'on obtient un chocolat, la probabilité qu'il soit sucré est 1/3 ; donc PCP_CPC(S) = 1/3
-
La probabilité d'obtenir une boisson sucrée est 5/9 ; donc P(S) = 5/9
As tu trouvé les mêmes conclusions que moi ?
Je fais un arbre et je l'envoie dans quelques temps.
-
-
MMiYo28 dernière édition par
oui, mais sauf pour P(T inter S) je n'ai pas compris, j'ai trouvé P (S sachant E) = 5/9
-
MMiYo28 dernière édition par
Reponse à Noemi,
Je propose, la probabilité d'obtenir un expresso sucré,
P (E inter S) = P (E) * P (S sachanrt E) = (1/2) * (5/9) = (5/18).
-
Zorro dernière édition par

Bon voici l'arbre que je trouve :
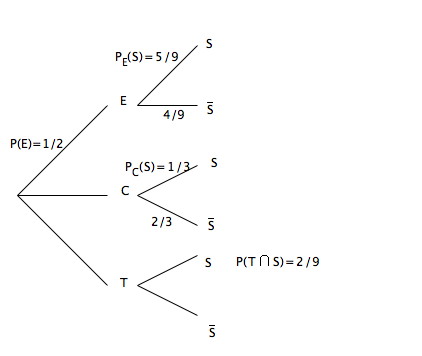
-
Zorro dernière édition par

Maintenant , il faut traduire P(S) = 5/9
cela te permettra de trouver PTP_TPT(S)
-
Oui,
Tu peux résoudre la question 3 en prenant la probabilité d'obtenir une boisson sucrée.
-
MMiYo28 dernière édition par
Es-ce que je suis bien partie ?
P(S) = P(C ∩ S) + P( E ∩ S) + P (T ∩ S)
5/9 = P(C ∩ S) + 5/18 + 2/9
5/9 = P ( S) * P ( S sachant C) + 5/18 + 2/9
5/9 = 5/9 * P ( S sachant C) + 5/18 + 2/9
-
MMiYo28 dernière édition par
Zorro
Maintenant , il faut traduire P(S) = 5/9cela te permettra de trouver PTP_TPT(S)
Je propose :
P ( T ∩ S) = P( S ) * P (S inter T)
2/9 = 5/9 * P (S inter T)
P (S inter T) = 2/9 * 9/5 = 2/5
-
as-tu trouvé le 1/18 pour la probabilité d'obtenir un chocolat sucré ?
-
MMiYo28 dernière édition par
Noemi
as-tu trouvé le 1/18 pour la probabilité d'obtenir un chocolat sucré ?Non, mais je propose , mais j'ai reussi à calculer P ( C)
P (C∩S) = P(C) * P( S sachant C)
1/18 = P(C) * (1/3)P (C) = 1/18 * 3 = 3/18
-
Tu as P(T∩S) = 2/9, P(E∩S)= 5/18 et P(S ) = 5/9
donc P(C∩S) = ...
-
MMiYo28 dernière édition par
P(S) = P(T∩S) + P(E∩S) + P(C∩S)
5/9 = 2/9 + 5/18 + P(C∩S)5/9 - 2/9 - 5/18 = P(C∩S)
10/18 - 4/18 - 5/18 = P(C∩S)
P(C∩S) = 1/ 18
-
C'est juste.
-
MMiYo28 dernière édition par
Pour la question 5, je dois trouver P (S sachant T) ?
-
Question 5 : p(T sachant S)
-
MMiYo28 dernière édition par
.
-
MMiYo28 dernière édition par
Noemi
Question 5 : p(T sachant S)Je ne comprends pas
-
MMiYo28 dernière édition par
Je pense PT(S)