équation DM help : Aire BMI = 1/3 Aire ABCD (fonction)

ABCD est un rectangle tel que AB=6 cm et AD=4 cm.

Le point I est le milieu du côté [AD].

Où doit-on placer le point M sur le côté [CD] pour que l'aire du triangle BMI soit inférieure ou égale au tiers de l'aire du rectangle ABCD ?

On note DM = x.

:rolling_eyes:

BONJOUR

VOILA MON PROBLEME :

[ici tu mets ton énoncé]

J'ARRIVE PAS A FAIRE CECI :

[tu inclus ici la description du "ceci"]

J'AI ESSAYE CELA :

[tu inclus ici la description du "cela"]

Et merci d'éviter de poster le topic n'importe où sur le site : y'a des catégories pour ça. Je dirais que tu es en 3e...

Bon sérieusement, qu'as-tu essayé de faire ?

d'abord j'ai calculé l'aire du triangle ensuite j'ai calculé tous les aires des trois petits triangles qui sont autour du triangle BMI mais ensuite je ne comprend pas comment il faut faire.

tout cela en fonction de x ? montre un peu les expressions obtenues.

ah ben ça alors, y'a plus personne...

voici la figure avec une position possible pour M

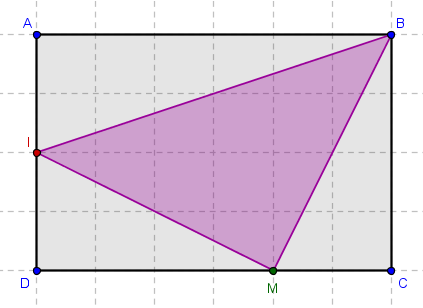
$fichier math$

ça fait un peu peur en gros comme ça... bon la position de M varie entre C et D

On repère sa position par rapport à D : c'est la signification de DM = x.

à l'aide de x, il faut que tu exprimesl'aire du triangle BMI.

desole j'etais chez mes grands parents
maisma prof de maths ma dit de d'abord calculer l'aire des trois petits triangles qui sont DIM, MBC et IBA.
DIM=x
MBC=?
IBA=6
et voila mais ensuite que faire?

he coucou peut tu me repondre SVP

oui elle a raison

tu trouves BIM en enlevant les trois petits triangles au rectangle ABCD

MBA est un triangle rectangle dont les côtés de l'angle droit sont BC=4 et MC... pour ce dernier, c'est BD - DM, non ? propose-moi une expression de MC en fonction de x.

l'aire de BIM est donc ...

peut tu SVP me donner d'autre indications mais BD-DM ce n'est pas possible car c'est la diagonale et puis si je fais BD-DM ca me donnera x comment calculer BMI apres

oui pardon, c'est DC - DM : tu vois bien que M est aligné avec D et C

bien MC = DC - DM

remplace par ce que tu "connais"

MC=DC-DM
x=6-x
comment faire

nonon MC n'est pas égal à x

il y a 6 entre D et C, et il y a x entre D et M

donc entre M et C il reste 6 - x.

c'est donc MC = 6-x.

maintenant à toi de me donner l'expression de l'aire de MBC en fonction de x

6-x=6-x
alors on en revient a quoi?

mais non : MC = 6-x y'a pas encore d'équation

je te demande l'aire de BCM : côté (de l'angle droit) fois autre côté (de l'angle droit), divié par 2 en fonction de x.

j'attends.

mais MC est égale a quoi

sa fait 6-x*4:2

à 6-x

x est une longueur comprise entre 0 et 6 cm

le problème c'est que manifestement ta prof ne t'a pas fait tracer quelques figures avec différentes valeurs de x.

deux secondes je te montre ce que c'est qu'un point mobile sur un segment... et les variations de l'aire que ça entraine.

tu as trouver la solution toi?

en vert la longueur x qui varie

en violet l'aire (qui varie conjointement)

fig 1

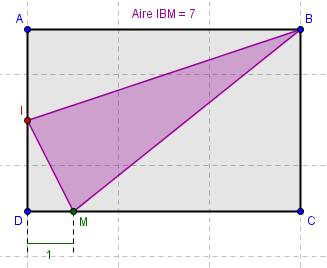
$fichier math$

fig 2

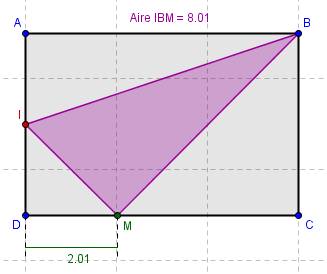
$fichier math$

fig 3

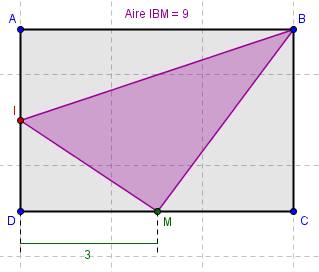
$fichier math$

fig 4

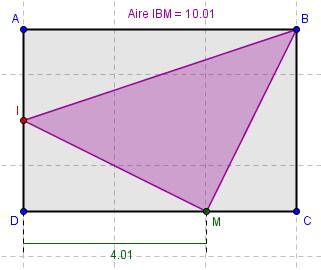
$fichier math$

fig 5

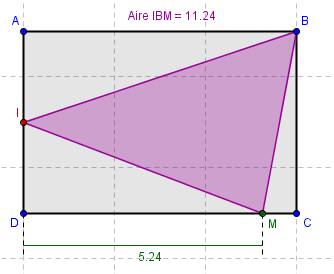
$fichier math$

voilà

pour l'aire de BCM, tu as trouvé (à l'oubli des parenthèses près)

Aire BCM = 2(6-x), après simplification.

et alors toute ces figure m'ammene a quoi vu qu'on ne connait pas la distance entre M et C ou sinon donne moi carrement la solution

ça te montre que MC dépend de la position de M sur le segment [CD]
l'aire violette aussi, dépend de cette position

cette position est déterminée par la longueur x entre D et M

donc tu as vu que aire BCM = 12 - 2x oui ?

maintenant peux-tu me donner l'expression de l'aire de BMI ?
(par soustraction...)

pourquoi 12 il viens d'ou ce 12
je suis perdue peut tu me faire un recapitulatif SVP

depuis le debut

on parle de l'aire de BCM. tu as dit : (6 - x)×4÷2 ça fait 12-
2x après calcul

c'est fait exprès pour que tu te poses des questions si j'écris ce genre de truc

maintenant tu me donnes l'aire de BMI ?

aire de BMI
aire de ABCD- ( aire de ABI+aire de BCM+aire de DMI)=aire de BMI donc
24-(6+(12-x)+x)=aire de BMI

deux secondes...

c'est 12 -
2x pour l'aire de BCM
j'ai oublié le 2 ci-dessus

l'aire de BMI est donc 6 + x en réduisant.

le dm est pour demain alors je dois donc le recopier ce soir alors pourrais tu me donner la reponse si sa ne te gene pas

lol

non.

je t'ai donné l'aire de BMI.

il faut que tu résolves aire BMI inférieure ou égale à (aire ABCD)/3

c'est une inéquation que tu as dû apprendre à résoudre.

non je n'ai pas appris comment resoudre ce genre d'inequation
24-(6+(12-2x)+x)=aire de BMI
comment fait on alors?

Où doit-on placer le point M sur le côté [CD] pour que l'aire du triangle BMI soit inférieure ou égale au tiers de l'aire du rectangle ABCD ?

il ne faut pas oublier que nous devons resoudre cette question comment faire?

La fin est dans cette discussion.