Les nombres carrés [Défi : 6ème]

Bonjour à tous !

Voilà, la professeur de maths de ma soeur (qui est en 6ème) a donné a tous ses élèves un défi a faire pendant ses vacances... Et il se trouve que même moi je n'arrive pas à le résoudre....

Ci dessou, le sujet et nos réponses:

" Quand tu multiplies un nombre par lui-même, tu obtiens un nombre carré. Si tu dispose d'un nombre carré d'objets, tu poeux les arranger en formant un carré. La série des nombres carrés est l'une des plus importante en maths. "

a) Ecris la liste des 15 premiers nombres carrés.

Pour cette 1ère question, nous avons mis ceci :
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225.

b) Soustrais ces nombres 2 par 2 et écris tes réponses sur une ligne. Arrives-tu à discerner une loi ?

*Nous avons donc soustrais 2 par 2 les nombres carrés :
1² = 1
2² = 4 donc 4-1 = 3

3²-2² = 5

3² = 9
4² = 16 donc 16-9 = 7

5²-4² = 9

5² = 25
6² = 36 donc 36-25 = 11

7²-6² = 13

7² = 49
8² = 64 donc 64-49 = 15

9²-8² = 17

9² = 81
10² = 100 donc 100-81 = 19

11²-10² = 21

11² = 121
12² = 144 donc 144-121 = 23

13²-12² = 25

13² = 169
14² = 196 donc 196-169 = 27

15²-14² = 29

15² = 225

Est-ce un bon début ? C'est pour discerner la loi que nous avons un problème...
Nous avons pensé tout d'abord qu'il pourrait peut-être s'agir de nombres premiers mais NON puique 2 de nos résultats que nous avons trouvé n'étaient pas cohérents : 15 et 17 (ils ne sont pas des nombres premiers !).
Ensuite nous avons vu que si l'on soustrais comme ceci :
Nombre pair - Nombre impair = Nombre impair. *

Est-ce que nos résultats sont bons ? Ou sommes nous sur la mauvaise voie ?

Merci de nous éclairer, nous sommes un peu perdu.. :rolling_eyes:

Bonjour,
Quelle est la question ?
Dans quelle classe es-tu ?
Observe :
5²-4² = 9 = 2*4 +1
Est-ce vrai pour les autres différences ?

PS : attention : tu oublies des différences : par exemple 3²-2² , ... 15² - 14²

Bonjour,

La question qui nous pose problème est la suivante : "Arrives-tu à discerner une loi ?" et moi je suis en 1ère S (LA HONTE..) et je n'arrive pas a répondre à cette question-ci.

mathtous
5²-4² = 9 = 24 +1
Est-ce vrai pour les autres différences ?
C'est à dire ? On doit faire par exemple 2² - 1² = 3 = 21 + 1 ?

Ps : Oui, j'ai modifié mon premier message que j'ai posté en rajoutant les soustractions manquantes

7²-6² = 49 - 36 = 13 = ??
Mais si tu es en première, tu dois pouvoir
prouverla loi.
En sixième, on peut s'aider d'un dessin.

Alors... 7²-6² = 49 - 36 = 13 = 6*2 + 1 ?

Ce que je ne comprends pas dans ce problème, c'est la loi que l'on essaie de nous faire ressortir.

Est-ce que la différence entre deux carrés consécutifs ne serait pas par hasard égale au double du plus petit nombre augmenté de 1 ?
Autrement dit :
si a est l'un des nombres et le suivant est donc a+1 , n'a-t-on pas :
(a+1)² - a² = 2a +1 ?
Egalité que tu peux démontrer en première.
Et en sixième, essaie de faire un dessin ( deux carrés l'un dans l'autre ).

En fait c'est cette égalité que nous devons démontrer à l'aide d'exemples : (a+1)² - a² = 2a +1 ?

Salut

En 6e, je pense que le prof voulait seulement faire observer que les différences entre les carrés consécutifs sont les impairs successifs.

La loi mentionnée par mathtousest plus précise et intéressante pour le calcul mental.

Ceci permet par ex sachant 15² = 225, de trouver de suite 17² sans multiplier (il suffit d'ajouter 31, i.e. 2×15+1) .

C'est vrai qu'en $strong>6^e$ on observe ou on montre sur un dessin, alors qu'en $strong>1^{re}$ on démontre.

visuellement, le "truc" de mathtousc'est :

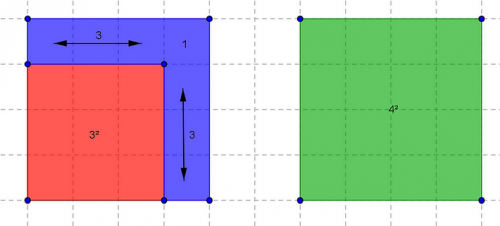
$fichier math$

[Illustration doublon avec le post ci-dessous - mais comme j'avais fait un dessin, je l'ai ajouté quand même... NdZ]

Citation
démontrer à l'aide d'exemplesLes exemples ne fournissent pas une démonstration.
En première, tu dois connaître les identités remarquables : (a+1)² - a² = ??

En sixième, tu peux observer le dessin suivant.
La différence entre les aires est la partie colorée : elles est constituée de 3 parties.

$fichier math$

Oui, là elle est en 6ème alors pour lui expliquer tous ça, c'est pas très simple, mais je pense y arriver quand meme.
Comment le montrer sur un schéma ?

Citation
En sixième, tu peux observer le dessin suivant.
La différence entre les aires est la partie colorée : elles est constituée de 3 parties.
Quelles sont les aires de chacune des portions colorées ?
Tu as bien reçu le dessin ?

L'aire du carré jaune et blanc est (a+1)(a+1)

Oui : l'aire du grand carré :
(a+1)(a+1) = (a+1)² : explication en sixième : c'est le plus grand des deux carrés.

Ah oui, alors dans l'expression : (a+1)² - a² = 2a +1; l'aire du grand carré est (a+1)² et l'aire du petit carré est a²

Comme on veut la partie colorée, on soustrait l'aire du grand carré - l'aire du petit carré, d'où (a+1)² - a² = 2a + 1

Je dois me déconnecter.
A+ si tu ne reçois pas d'aide.
Mais tu as Zauctore, tu es tranquille.

mathtous
Je dois me déconnecter.
A+ si tu ne reçois pas d'aide.
Mais tu as Zauctore, tu es tranquille.

Merci dans tous les cas pour votre aide.

Citation
Comme on veut la partie colorée, on soustrait l'aire du grand carré - l'aire du petit carré, d'où (a+1)² - a² = 2a + 1Là, tu calcules la différence.
Mais pour utiliser le dessin, tu dois expliquer que la partie colorée est justement la différence des deux carrés.
Puis, exprimer cette partie colorée en utilisant le dessin : 2 rectangles identiques et un tout petit carré.

D'accord. Mais c'est tout ce qu'il faut dire alors concernant cette loi ? A-t'elle un nom précis ?

C'est déjà bien.
Il faut trouver une bonne rédaction pour que les explications soient claires.

A d'accord. Pour la rédaction, il faut d'abord mettre la formule :
(a+1)² - a² = 2a + 1
et la vérifier avec la liste des carrés jusqu'à 15 comme ceci :

2² - 1² = 21+1 = 2+1 = 3
3² - 2² = 22 + 1 = 4+1 =5
et ainsi de suite non ?
Ensuite on mets un dessin pour illustrer la loi ?
Celui-ci me semble bien étant donné qu'il généralise la loi :
[quote=mathtous]
Citation

$fichier math$

Non : il faut distinguer le raisonnement de ce qu'on observe.

On donne quelques exemples ( normalement ils sont déjà tous écrits avant ).

Il sembleque la différence entre les carrés des deux nombres soit égale au double du plus petit augmenté de 1.
3) On donne le dessin et on dit que :
a) on voit les deux carrés : le grand et le petit en blanc.
b) La différence est la partie colorée.
c) Cette différence est la somme de deux rectangles de a sur 1 et du carré de 1 sur 1
d) elle vaut bien le double du petit nombre augmenté de 1.

On peut donner la formule en dernier en indiquant que a est le plus petit des deux nombres et que a+1 est le plus grand ( le suivant ).

Je n'ai pas très bien saisi le petit c quand vous dites " de a sur 1 et du carré de 1 sur 1" ?

Je veux dire que les dimensions d'un rectangle sont a et 1 ( longueur et largeur ).
Tu n'as jamais entendu l'expression "un rectangle de 3m sur 1.5m " ?
Et pour le carré jaune foncé : son côté mesure 1.
Comme indiqué sur le dessin.

Ah oui, je n'avais pas compris. Oui je vois maintenant.
Et quand vous dites "elle vaut bien le double du petit nombre augmenté de 1" , vous parlez de la différence ou de la somme ?

Des deux mon capitaine.
La
différencedes deux carrés est en jaune ( clair et foncé ).
Cette
différenceest formée de la
sommedes deux rectangles et du tout petit carré : a1 + a1 + 1*1 = 2a+1

D'accord, d'accord !
Eh bien, je sens que pour lui expliquer je vais m'amuser..

Merci Beaucoup de votre aide !
A bientôt sur le forum.

De rien
A+
Si besoin, tu peux aussi me joindre ici :
http://dmat.perso.neuf.fr/forum/forum.php

Ah génial, c'est votre forum ? Je peux y poster un sujet si j'ai besoin ?

Oui.
Tu peux même te promener sur l'ensemble du site.

Très bien !
J'y vais faire un tour dès que j'en aurais terminé avec ce problème...

A+