Lecture graphique, limites et variations d'une fonction

Bonjour à tous , j'aurais souhaité un petit peu d'aide , merci d'avance .

La figure représente la courbe C d'une fonction f dérivable sur R .

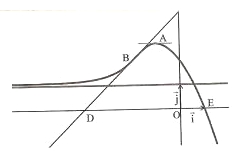
$fichier math$
Les points E(1;0) , A(-1;e) et B(-2;2) sont des points de C

La tangente à C en A est paralléle à l'axe des abscisses

La tangente à C en B passe par D(-4;0)

La droite d'équation y=1 est asymptote à C en -∞

La fonction f est strictement croissante sur ]-∞;-1] et strictement décroissante sur [-1;+∞[

1.a) Donner les valeurs de f(-2) , f(-1) , f(1) ainsi que la limite de f en -∞ .

b) Donner en justifiant vos réponses , les nombres f'(-1) et f'(-2)

2. Soit g la fonction définie par g(x)= ln(f(x)) et delta sa représentation graphique .

a) Déterminer l'intervalle I de définition de g.
Calculer les limites de g en -∞ et +∞
En déduire les asymptotes à la courbe delta en précisant un équation pour chacune d'elles .

b) Exprimer g'(x) à l'aide de f(x) et de f'(x) .
En déduire le tableau de variation de g

c) Déterminer g(-2) et g'(-2) , puis une équation à la tangente à delta au point B' d'abscisse -2 .

alors pour la question 1.a) j'ai trouvé : f(-2) = 2 , f(-1) = e et f(1) = 0
pour la limite je vois pas comment faire ..

quelqu'un peut m'aider ?

?

Re Bonjour,

Pour la limite, quelle valeur vaut y si x tend vers -∞ ?

Aucune idée ... je vois déjà pas comment calculer la limite à partir d'un graphique ...

Si x = -5 ; y = ...... ?
si x = -8 ; y = .... ?

Compléte

Si x = -5 ; y = -5 ?
si x = -8 ; y = -8 ?

Comment peux-tu trouver des valeurs négatives pour y, la courbe est au dessus de l'axe des abscisses ??

vérifie.

si x=-5 , y = 0 et si x=-8 , y = 0 ?

pourquoi y = 0 ???

Je me suis trompée .. mais je peux pas dire quand x=-5 et x=-8 ce que vaut y ...

Pourquoi, tu ne peux pas lire sur le graphique ?

ahh si y vaut 1 ?

y=1

oui, y = 1 c'est une asymptote horizontale.

donc la limite de f en -∞ est égal à 1 ?

Oui, c'est la limite.

et c'est juste ce que j'avais trouvé : f(-2) = 2 , f(-1) = e et f(1) = 0 ?

et pour f'(-1) et f'(-2) ?

Pour la lecture graphique de l'ordonnée des points, c'est juste.

pour f'(1) et f'(-2) c'est la pente de la tangente à la courbe.

c'est la pente de la tangente à la courbe ? je comprend pas trop

Le coefficient directeur de la tangente à la courbe.

f'(-1) = e
f'(-2) = 0 ?

f'(-1) = e Non, quel est le coefficient directeur de la droite passant par A ?

f'(-2) = 0 ; Non, quel est le coefficient directeur de la droite passant par B ?

Aucune idée ..

je comprend rien

Pour déterminer le coefficient directeur d'une droite,
A partir d'un point A de la droite tu dois rejoindre un point B de cette droite avec deux possibilités de déplacement, soit verticalement, soit horizontalement.
Exemple :
Pour la droite passant par B.
Tu pars du point B (abscisse -2)
Tu te déplace verticalement vers le haut de deux unités (y = +2), puis tu te déplaces horizontalement jusqu'à atteindre un autre point de la droite de 2 unités ( A vérifier !!) ( x = 2)
donc f'(-2) : déplacement selon y / déplacement selon x ici 2/2, soit f'(2) = 1.

J'ai fait le méme scénario pour A et je trouve f'(-1) = e

Comment est la tangente au point A ?

paralléle à l'axe des abscisses

Oui

Si tu écris f'(-1) = e cela veut dire que en partant du point A, tu montes d'une distance e puis tu te déplaces de une unité, tu te trouves sur la tangente.
Est ce possible ? vu que la tangente est horizontale

Oui j'avais fait ce déplacement là .. Mais je vois pas comment me déplacer sinon

Si tu fais ce déplacement, tu n'es pas sur la tangente.

Pour rester sur la tangente, on ne dois pas de déplacer verticalement, soit y = 0 et x = 1 ou 2 ou ....
donc f'(-1) = 0/2 = 0

D'accord ! On peut reprendre demain ?
Bonne soirée et merci

A demain.
Bonne nuit.

Bonjour ,

Je peux avoir quelques indications pour la question 2.a) ?

Bonjour,

ln(x) définie si .......
ln(f(x)) définie si .....

Ce n'est plutot définie sur ?
ln(x) définie sur ]0;+∞[
ln(f(x)) définie sur : je sais pas

ln(x) définie si x > 0, soit sur ]0 ; + ∞[
ln(f(x)) définie si f(x) >0, soit sur ...... (Utilise la représentation graphique)

ln(f(x)) définie si f(x) >0, soit sur ]-4:1] ?

Non,

Pour quelles valeurs de x, le graphe de la fonction est au dessus de l'axe des abscisses ?