Trouver les coordonnées d'un point .

La figure représente un parallélépipéde rectangle où AE = AB = 3 , L est le milieu de [FG] , N est le milieu de [AD] , M est le point tel que Vecteur EM = 3/4 de vecteur EH , et P est le point tel que vecteur BP = 1/4 de vecteur BC .

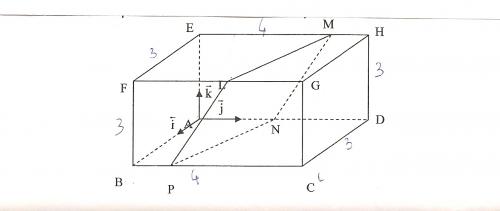
ABCDEFGH représente un parallélépipéde rectangle

Je voudrais juste un peu d'aide pour trouver les coordonnées des points L , M , N , et P .

Merci d'avance

Re Bonjour ( A ne pas oublier !!!)

Pour les coordonnées des points, cela peut se résoudre comme un problème de déplacement, sachant que l'on part de l'origine, ici A et que l'on commence par x, puis y puis z
Pour atteindre le point L
de A, 3 unités sur x soit au point B ; x = 3
puis 2 unités selon y (L est au milieu de [FG] ; y = 2
puis 3 unités selon z ; z = 3
Donc L (3;2;3)

Re bonjour ,

D'accord pour L
Donc pour M , je pars de A , 3 unités sur x ; x=3
3 unités selon y ; y=3
3 unités selon z ; z=3
M(3;3;3 ) ?

Non,

Pourquoi ce déplacement selon x ? x = 3 ?
Le point trouvé est sur le segment [FG]

x=0 alors ?

Oui
M(0;3;3)

Pour N jai trouvé (3;2;0) Et pour P (3;1;0) ?

Vérifie ton calcul pour N.

N(0;2;0) ?

C'est juste.

Et vous pouvez m'expliquer comment calculer une longeur ? LM ?

Calcule les coordonnées du vecteur , puis sa norme.

sa norme ? c'est quoi déjà ?

Tu n'as pas un cours, un livre ?
vect AB (xB-xA; yB-yA; zB-zA)

AB² = (xB-xA)² + (yB-yA)² + (xB-xA)²

Si . Merci beaucoup pour l'aide . Merci pour tout .