Ligne de niveau {M tq MA/MB = 3} ; deux méthodes
-
Kkokoworld dernière édition par
Bonjour! Alors voila j'ai un exercice et je bloque complètement.
"Dans le plan rapporté à un repère orthonormal, on considère les points A(1 ; 2) et B(-3 ; 0). On cherche à déterminer le lieu L des points M du plan tel que
mamb=3\frac{ma}{mb}=3mbma=3.
PARTIE A:Méthode géométrique.
1) Démontrer que M appartient à L équivaut à :
(ma⃗−3mb⃗)⋅(ma⃗+3mb⃗)=0(\vec{ma}-3\vec{mb})\cdot(\vec{ma}+3\vec{mb})=0(ma−3mb)⋅(ma+3mb)=0
2) En déduire que M appartient à L équivaut à:
mi⃗.mj⃗=0\vec{mi}.\vec{mj} = 0mi.mj=0
où I est le barycentre du système {(A:1),(B;-3)} et J le barycentre du système {(A;1),(B;3)}.3) Calculer les coordonnées des points I et J.
4) Déterminer et construire L
PARTIE B:Méthode analytique
1) En notant (x;y) les coordonnées du point M, exprimer les distances MA et MB en fonction de x et y.
2) Démontrer que M appartient à L équivaut à
x2+y2+7x+12y+192=0x^2+y^2+7x+\frac{1}{2}y+\frac{19}{2}=0x2+y2+7x+21y+219=0
3) En utilisant les formes canoniques des trinômes du second degré en x et y, déterminer et construire L
4) Donner une équation cartésienne de la droite (AB).
5) Déterminer par le calcul les coordonnées des points d'intersection de L avec (AB), puis vérifier que ce sont les points I et J définis dans la partie A."
Merci d'avance

-
Zauctore dernière édition par

Salut
N'as-tu rien fait ?
Pour la question 1 de la première partie, tu peux partir du produit scalaire donné, le développer et retrouver le rapport initial MA/MB = 0.
La question 2 est une simple réécriture de la 1, avec les barycentres définis par l'énoncé.
La 3e est une question de cours sur les coordonnées du barycentre.
Le produit scalaire nul de la question 2 définit clairement le lieu des points M (cf collège... si si) : cela répondra à la 4e question.
A toi.
-
Kkokoworld dernière édition par
Pour la 1 c'est ok, mais pour la 2, j'ai utilisé la relation de Chasles en remplaçant mi⃗\vec{mi}mi par (ma⃗+ai⃗\vec{ma}+\vec{ai}ma+ai) et mj⃗\vec{mj}mj par (ma⃗+aj⃗\vec{ma}+\vec{aj}ma+aj) et après j'ai développée (ma⃗+ai⃗\vec{ma}+ \vec{ai}ma+ai).(ma⃗+aj⃗\vec{ma}+ \vec{aj}ma+aj) mais après je suis coincée.
-
Zauctore dernière édition par

salut
attention à ce que tu fais : par définition, I est barycentre du système {(A ; 1) , (B ; -3)} si et seulement si...
-
Kkokoworld dernière édition par
si et seulement si ia⃗+3ib⃗=o⃗\vec{ia}+3\vec{ib}=\vec{o}ia+3ib=o
-
Zauctore dernière édition par

non, vois ici.
c'est IA - 3IB = 0
maintenant avec un coup de Chasles, intercalant I dans MA - 3MB...
rq : je note en grasles vecteurs.
-
Kkokoworld dernière édition par
Je n'arrive pas a voir le rapport entre les barycentres donnés et le produit scalaire mi⃗.mj⃗=0\vec{mi} .\vec{mj} =0mi.mj=0

-
Zauctore dernière édition par

Salut
Je rappelle que je note en grasles vecteurs.
Chasles : MA- 3 MB= MI+ IA- 3 MI- 3 IB= -2 MI+ IA- 3 IB
or IA- 3 IB= 0 car I est le bary de (A, 1) et (B, -3).
Il reste donc - 2 MI.
Dans le produit scalaire (MA- 3 MB).(MA+ 3 MB), tu peux alors remplacer et ainsi écrire
(MA- 3 MB).(MA+ 3 MB) = -2 MI.(MA+ 3 MB)
A toi pour la suite.
-
Kkokoworld dernière édition par
Ok, j'ai compris.
Après je fais la même chose avec ma⃗+3mb⃗\vec{ma} +3\vec{mb}ma+3mb en intercalant J cette fois-ci.
Sa donne donc −2mi⃗.4mj⃗=0-2\vec{mi} .4\vec{mj} =0−2mi.4mj=0
Donc M appartient à L équivaut à mi⃗.mj⃗=0\vec{mi} .\vec{mj}=0mi.mj=0
-
Zauctore dernière édition par

Exactement !
Tiens, les barycentres annoncés :
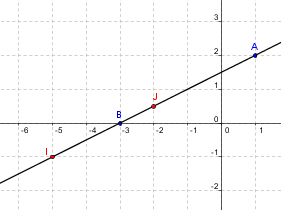
On dit que I et J divisent [AB] dans le rapport 3:1, on a IA/IB = 3 = JA/JB
Il n'y a que deux tels points sur (AB).Maintenant, tu sais où se situent tous les points M du plan tels que MI.MJ = 0 ?
-
Kkokoworld dernière édition par
Les points M du plan se situent donc sur la médiatrice de IJ?
-
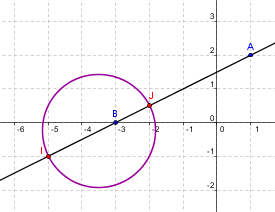
Zauctore dernière édition par

Pas du tout : c'est un cercle ! car la condition se traduit par le fait que l'angle IMJ reste droitlorsque M varie.
Rappelle-toi ce théorème de 4e :
dans un triangle rectangle, le sommet de l'angle droit est situé sur le cercle circonscrit.
-
Kkokoworld dernière édition par
A oui c'est vrai, Donc Puisque M appartient à L, L c'est le cercle de diamètre IJ
-
Zauctore dernière édition par

Ce qui fait que l'on a en définitive la configuration "bielle" (chemin de fer à vapeur...) ci-dessous illustrée :
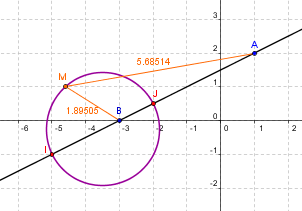
avec l'exemple montré, on a 5,68514÷1,89505 ≈ 2,9999947 c'est-à-dire 3.
-
Kkokoworld dernière édition par
Ok j'ai compris.
Ensuite pour la 1) de la partie B, pour exprimer MA et MB, j'utilise la formule MA=√(xA-xM)²+(yA-yM)² et pareil pour MB en remplacant xA et yA par xB et yB.
-
Zauctore dernière édition par

C'est ce qui est demandé.