trapeze -thales

On consière un trapèze ABCD de bases [AB] et [CD] mesurant 11 cm pour [AB] et 15 cm pour [CD]. On place le point M sur [AD] et le point N sur [BC] de façon que les droites (MN) et (AB) soient parrallèles et on donne les mesures suivantes AM = 6 cm, MD = 2 cm et BN = 7 cm

La parrallèle à (BC) passant par A coupe (MN) en I et (DC) en J

Faire la figure
calculer dans l'ordre DJ, MI, MN, AI, AJ,NC

Bonjour ? M***e ?

Adele75, je sais qu'on est au XXIe siècle, mais quand enfin même... ça se fait encore de respecter un minimum les usages !

bon après ça, tu postes un exo c'est bien gentil ; mais tu ne dis pas ce qui te gêne, ce que tu as fait ou pas : bref tu ne permets pas de t'aider. car si c'est pour que quelqu'un se dévoue pour faire le boulot à ta place, c'est pas le bon coin ici !

je peux mettre la figure pour commencer, parce que je suis bien luné ce matin :

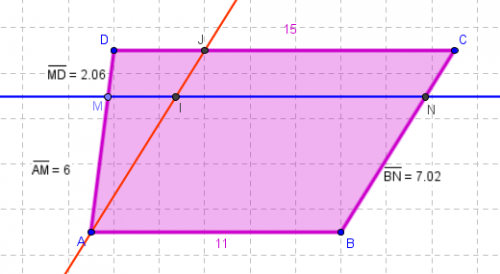
$fichier math$

(avecGeoGebrabien entendu).rq : orthographe de *parallèle*, avec un seul r

Maintenant pour ton exo, faut penser aux propriétés du parallélogramme, et au théorème de Thalès.

Bonjour,

Désolé d'avoir été involontairement impolie. J'étais perdue dans mes pensées avec cet exo.

En fait pour calculer DJ j'ai proposé :

Par hypothese ABCJ est un quadrilatère, or si un quadrilatère a ses deux coté opposés 2 à 2 alors c'est un parrallèlogramme. Par hypothèse, AB = 11 cm alors jc = 11 cm donc dc = 15-11 donc dj = 4 cm.

Mais je n'ai pas démontrer que les deux cotés étaient parralèles et que JC avait la même mesure que AB.

pour MI
on a le triangle ADJ
avec A M D alignés
avec A I J alignés

(MN) // (DC)
I sur (MN) avec M I N alignés
J sur (DC) avec D J C alignés
j' applique le théorème :
AM/AD = MI/DJ

après je bloque. Faut-il à chaque fois appliquer le théroreme de Thalès ?

Merci

Adèle. Encore désolée !!!!

re.

tu fais un contresens dans la propriété que tu cites : c'est lorsqu'un quadrilatère a ses côtés opposés parallèles que tu peux affirmer qu'il s'agit d'un parallélogramme. c'est le cas ici, par le fait du trapèze (ses bases sont parallèles) et par définition de la droite (AJ).

donc ABCJ est un parallélogramme.

maintenant tu peux en déduire très simplement DJ qui est égal à DC - JC.
c'est ce que tu as fait.

tu peux alors calculer MI avec thalès. il faut écrire les rapports égaux et faire un bête produit en croix : AM/AD = MI/DJ devient 6/8 = MI/4.
la valeur de MI "saute aux yeux".

MN est une simple addition MI + IN.

AI se trouve immédiatement en expliquant la nature de ABNI ; on trouve AJ de même.

NC est égal à IJ...