géometrie : prouver qu'un triangle est équilatéral

bonjour.

je vous demande (S'il Vous Plait) de bien vouloir m ' aidé

car j'ai une figure a dessiné :

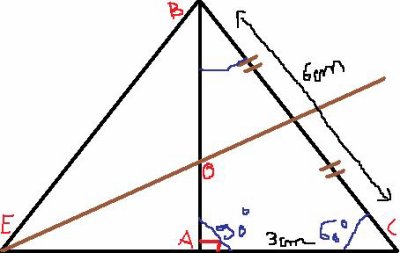
ABC est un triangle rectangle en A
AC =3cm et BC = 6cm

on m'a demander de calculer l'arrondi au mm de AB, j'ai trouvé ≈52 mm
puis je dois calculé le cos C et sa mesure en degrés , j'ai trouver cos C≈0.1 et C°≈60.
puis on me demande de tracer la médiatrice de [BC] elle coupe (AC) en E et (AB) en O : je l'ai fait.

mais le problème est la : on me demande de démontrer que le triangle BEC est isocèle, puis qu'il est équilatéral.

je le vois qu'il est isocèle et équilatéral mais je ne sais pas comment l'expliqué .

pouvez vous m'aider ??

ps= j'ai mis 'un schémas ici www.***.skyblog.com car je ne sais pas comment faire une figure sur ce site .

[lien supprimé par la modération, NdZ]

salut

le schéma annoncé est :

$fichier math$
pour inclure une image dans une discussion du forum, on peut cliquer sur le lien bleu sous le cadre de saisie "Ajoute une image" (ouvrir la fenêtre "en grand" et suivre les instructions).

nb : cos C = 0,5 (valeur exacte) et angle C = 60°, valeur exacte aussi.

ce sont des égalités, pas des approximations.

pour ton pb : il existe une très importante propriété de la médiatrice d'un segment.

"la médiatrice de [BC] est le lieu des points équidistants de B et C."
cela signifie que si P est sur cette médiatrice, alors PB = PC (et réciproquement).

c'est ce qu'il faut utiliser ici, conjointement à des propriétés angulaires...

donc si e est sur la médiatrice ????

hé bien, puisqueE est sur la médiatrice de [BC], tu peux affirmer que EB = EC, c'est-à-dire que EBC est isocèle en E.

à toi pour la suite (angles...) !

Bonjour,

Le point E est sur la médiatrice de [BC], donc EB = EC
et le triangle EBC est ......

ok merci

re (dsl si je vous pose trop de question) :rolling_eyes:
puis pour démontrer que le triangle est équilatéral , il faut dire comme la droite BA est (hauteur médiatrice et médiane dans le triangle BEC) ,alors elle coupe l'angle B en deux donc l'angle B = 60° . et comme dans un triangle la somme des 3 angle vaut 180° alors l'angle E vaut aussi 60°. et comme dans un triangle équilatéral tout les angle valent 60 ° alors le Triangle BEC est équilatéral ??? c'est ça ???

le sais que la droite (BA) est médiane hauteur médiatrice mais comment le démontrer .

pour le 1er comme Le point E est sur la médiatrice de [BC], donc EB = EC
et le triangle EBC est isocèle c'est ça ,?

ensuite :
alors comme le triangle BEC est isocèle en E et comme l'angle C = 60 °
donc l'angle B = aussi 60°
et comme la somme des trois angle = 180 alors l'angle E = donc 60 °
alors comme tout les angle = 60 ° alors le triangle est équilateral ? c'est sa ??
?

Tu as démontré que le triangle EBC était isocèle en E,
donc que peut-on dire de l'angle EBC et de l'angle ECB ?
Et
l'angle ECB = ...°
donc ....

on peut dire que l'angle EBC= 60° et l'angle ECB = 60 °
et
l'angle ECB= 60 °
donc le triangle est équilatéral .

:rolling_eyes:
il y a une autre petite question (dsl si j'en n'ai fait trop )
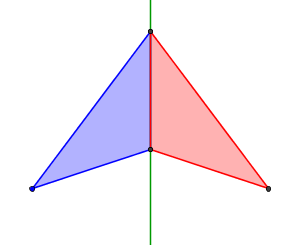
on me demande de citer une transformation du plan par laquelle le triangle BCO a pour image le triangle BOE. en préciser l'élément caractéristique .

??

c'est ce genre là :

$fichier math$

Bonjour,

Pour savoir comment envoyer un schéma et quels scans sont tolérés ici, lire le sujet écrit en rouge dans la page d'accueil et qui a pour titre :

Inserer une image dans un message !lien : http://www.math...et-4932.html