Déterminer l'expression de la fonction affine passant par deux points donnés

bonjour
j'ai un exercice qui me pose problème
tracer, dans un repère orthonormé d'unité 2cm, la courbe représentative de la fonction f définie par f(x)=1/x sur [-4,4]. Placer les points A et B d'abscisses respectives 2 et 1/2 puis déterminer la fonction affine g représentée par la droite (AB). La droite (AB) coupe l'axe des abscisses en M et des ordonnées en N.
a)Déterminer les coordonnées des points M et N
b)Montrer que les segments [MN] et [AB] ont le même milieu
en déduire, en fonction des valeurs de x, la position de la courbe représentative de la fonction f par rapport à la droite (AB)

j'ai trouvé les ordonnées de A et B A(2,1/2) B(1/2,2)
g(x)= Mx + P M coefficient directeur et P ordonnée à l'origine
pour M j'ai trouvé -1 j'ai fait y(B)-y(A)/x(B)-x(A)
mais je suis bloqué car je ne sais plus comment trouver P
merci de m'aider

Bonjour utilise le fait que A ∈ (AB) ... ce qui signifie que les coordonnées de A répondent à l'équation de la droite (AB).

Cela te donne une équation qui te permet de déterminer p.

si je comprends bien pour A x= 2
donc g(x)=-1(2)+P
g(2)=-2+P
mais je ne sais pas combien vaut g(2)?

si j'ai compris l'équation je dois prendre les coordonnées de A
A(2,1/2)
1/2=M(2)+P
1/2=-1(2)+P
p=5/3

Tu as trouvé A(2 ; 1/2)

La droite (AB) a pour équation : y = -x + P

Or, A ∈ (AB) ⇔ $y_A$ = $x_A$ + P ⇔ ... tu remplaces par les coordonnées de A

erreur P=5/2

J'ai répondu en même tps.

Citation

A(2,1/2)
1/2=M(2)+P
1/2=-1(2)+P

p=5/
3

Vérifie ton calcul

Oui c'est correct

(AB) : y = -x + 5/2

merci je continue l'exercice et si je ne trouve pas le reste je reviens

pour le a) M(xm;ym)pour plus de comprehension
g(x)=ax+p car je vais confondre M le point d'ordonnée 0 et M le coefficient directeur
M le point intersection de (AB) et des abscisses
M(x;0)
g(M)=0=-1x+5/2
= -x+5/2
x=5/2
M(5/2,0)

N point intersection de (AB) et des ordonnées
N(0,x)
g(N)=-1(0)+5/2=5/2
N(0,5/2)
pour le b)
vecteurNB=vecteur AM
(xN-xB,yN-yB)=(xM-xA,yM-yA)
(1/2-0,2-5/2)=(5/2-2,0-1/2)
(1/2,-1/2)=(1/2,-1/2)
est-ce bon
mais je bloque sur l'inéquation 1/xinférieur à 5/2-x
j'ai mis 1/x+x inférieur 5/2 mais après je ne trouve pas

M( 5/2 ; 0 ) et N( 0 ; 5/2 )

C'est correct

Citation
b)Montrer que les segments [MN] et [AB] ont le même milieu
La méthode la plus simple serait de déterminer les coordonnées du point I milieu de [AB] et du point J milieu de [MN] puis de vérifier qu'ils sont confondus. Qu'en penses-tu ?

exact je m'y mets
mais peux tu m'aider pour l'inéquation?

En seconde, tu ne sais pas résoudre cette inéquation.

Dans la dernière question on attend de toi une résolution graphique je pense.

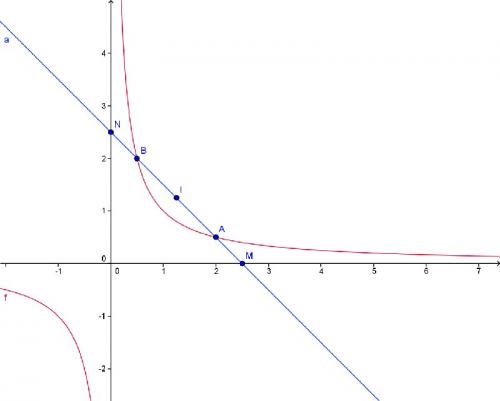
$fichier math$

Sur ]-∞;0[ Cf est ... de D

En 0, f n'est pas définie, on ne peut pas comparer Cf et D

sur ]0;...[ Cf est ... de D

...

pour l'inéquation
1/x inférieur à 5/2-x
1/x+x inférieur à 5/2
1+xcarré sur x inférieur à 5/2
mais après je suis bloqué
merci pour ton autre réponse

Iron
En seconde, tu ne sais pas résoudre cette inéquation.

Dans la dernière question on attend de toi une résolution graphique je pense.
Je te montre pourquoi : La position de Cf et de D dépend du signe de f(x)-D(x)

f(x)-D(x) = 1/x + x - 5/2

Cf est au dessus de D si et seulement si f(x)-D(x) > 0 cad si et seulement si :

Si x > 0

1/x + x - 5/2 > 0 ⇔
x (1/x + x - 5/2) > x × 0 ⇔ (j'ai multiplié par x des deux cotés, x positif conserve l'ordre)

1 + x² - (5/2)x > 0

il faudrait que tu saches factoriser le membre de gauche qui est du second degré ... ce que tu apprendras l'an prochain.

Travaille à partir du graphique

on me demande de résoudre algébriquement l'inéquation
je suis arrivé à 1 inférieur à (5/2-x)x

Je vais devoir quitter ...

Si tu veux résoudre algébriquement l'inéquation, tu peux utiliser le graphique pour déterminer les racines (valeurs qui annulent) du terme 1 + x² - (5/2)x

elles correspondent aux abscisses des points d'intersection, soit 1/2 et 2

tu peux alors factoriser ce terme

1 + x² - (5/2)x = (x - 1/2) (x - 2)

Attention, pour la résolution, il faudra discuter séparément pour x<0 et pour x>0.

car pour passer de
f(x) - D(x) < ou > 0

à

1 + x² - (5/2)x < ou > 0

on multiplie par x et le signe de l'inégalité change ou pas selon le signe de x !

à moins que l'on ne te demande de le faire que dans ]0;+∞[

Ca me semble difficile pour la 2nde.

merci pour ton aide

Tu as réussi ?

oui c'est sympa l'aide qu'on peut avoir sur le site