Calcul d'aire et périmètre d'un triangle à partir de ses médianes

Bonjour

Après 2 jours de recherches acharnées dans mes cours, je n'arrive pas à

calculer le périmètre et l'aire d'un triangle sachant que j'ai uniquement les médianes
comme indication. J'ai déjà cherché avec le théorème des médianes sans gros succès (recherches plus ou moins hasardeuses). Auriez-vous une astuce pour faire ce calcul?

Merci d'avance

salut

c'est un problème intéressant ! il faut continuer à chercher.

une indication de la réponse avec cette simulation GeoGebra :

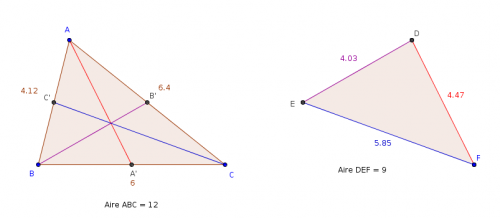
$fichier math$

joker: y a-t-il la formule de héron dans cette indication

sans doute !

mais pardon, je voulais juste faire observer le lien entre l'aire du triangle initial ABC d'une part, et d'autre part celle du triangle DEF formé avec les médianes du premier.

ça permet d'avoir une idée du résultat (cela s'appelle conjecturer), ce qui peut éventuellement guider une démonstration ultérieure.

j'ai une démonstration (n'utilisant que des notions très simples) du lien entre les aires des deux triangles, à base de la figure classique :

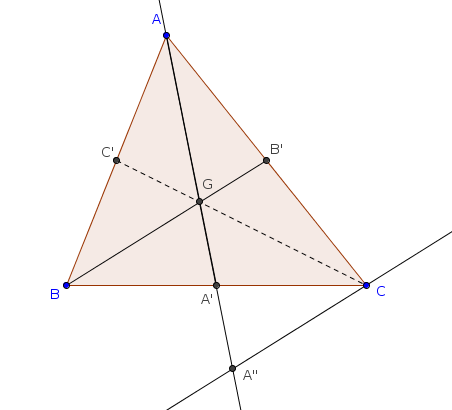
$fichier math$
c'est le triangle A''CG qui donne la réponse.

donc si j'ai compris, l'aire du triangle des médianes vaut 3/4 du premier triangle?

Je n'ai pas bien compris la relation avec A''

voilà, l'exemple te met sur la voie du rapport des aires : le 3/4 que tu annonces.

mais à ce stade, ce n'est qu'une conjecture, obtenue grâce aux valeurs fournies par GeoGebra

le problème est de démontrer cette conjecture ; pour cela, j'introduis la parallèle à (BB') passant par C, qui coupe la médiane (AA') en A''.

je te laisse chercher le lien entre

1° le triangle A''CG et le triangle des médianes comme tu dis

2° le triangle A''CG et le triangle ABC.

cela établira le lien entre le triangle initial ABC et le triangle des médianes.

ps : A', B' et C' sont bien entendu les milieux des côtés de ABC.

1°) A''CG c'est le triangle des médiane avec ses cotés réduit à 2/3

2°) (je ne vois que ça) c'est ABC mais réduit par 2

Donc grace à ça, si je prend 2/3 des médianes, puis que je multiple par deux, cela me donne les coté du triangle principal?

pour 1°, tu as vu juste

donc tu peux écrire Aire (triangle des médianes) =
...Aire A''CG.

pour 2°, il n'y a pas de proportionnalité entre ces deux triangles, hélàs ! mais en termes d'aire, entre A''CG et ABC il y a une relation simple.

hé non : pour ta question - on s'occupera de ça plus tard.

nb : je te proposerai une autre approche plus "1re S" par la suite (c'est-à-dire : calculs, calculs...)

1°)Aire (triangle des médianes) = 2/3 Aire A''CG.

2°)c'est pour ça que ça ne marche pas avec le théorème :frowning2:

je ne vois rien d'autre :frowning2:

1° : oh non ! tu as le rapport 3/2 pour les côtés , donc les aires sont dans le rapport 9/4 !!!
(et fais gaffe an sens : quel est le plus "grand", de A''CG ou du tr des médianes ?)

2° : vois-tu que Aire(A''CG) = Aire(BCG) ? ... donc ... ?

1°) oups je suis allez trop vite

2°) Ah oui je viens de voir avoir le parallélogramme A"CGB

Donc BC =A'C et pour A'C on utilise petit théorème de la médiane :
A"C² + CG² = 2CA'² + CG²/2 (théorème différent du forum mais c'est le même calcul)

humm pour l'instant ne nous égarons pas et contentons-nous des aires :

on a 1° : Aire(tr des médianes) = 9/4 Aire(A''CG)

et 2° : Aire(A''CG) = 1/3 Aire(ABC) t'es d'accord ?

d'où... le rapport 3/4 subodoré à16:24 !

Or donc, tu connais les longueurs des trois médianes ; via Héron, tu obtiens l'aire du triangle des médianes, et ainsi celle de ABC.

Zauctore

et 2° : Aire(A''CG) = 1/3 Aire(ABC) t'es d'accord ?

comment on fait pour trouver le 1/3 ?

Utilise BCG.

d'accord, puis après pour le périmètre je fais comme je pensait à 17h27?

oui c'est la 2e approche, très calcul-calcul, que j'évoquais tout-à-l'heure.

la formule de la médiane sous la forme m²_A = b²/2 + c²/2 - a²/4 permet d'écrire 3 équations d'inconnues a², b² et c² : c'est un système que tu dois savoir résoudre.

tu en déduiras a, b et c ; d'où le périmètre de ABC.

il n'y a pas plus simple?

comme BC = 2A'C
d'où A"C² + CG² = 2CA'² + AG²/2

si si bien sûr, autant exploiter à fond la figure-clé ci-dessus, en appliquant le théorème de la médiane à CA' dans A''CG (avec à chaque fois les 2/3 des médianes données).

j'ai mentionné à 17:55 la méthode utilisée habituellement sans la figure en question. il me semble que c'est généralement celle qu'on peut trouver sur le net.

merci beaucoup

Je t'en prie.

Maintenant un prolongement (qu'on ne trouve pas partout ) :

connaissant les longueurs des trois médianes, comment tracer un triangle ABC convenable ?

la solution est donnée par les 4/3 des médianes du triangle des médianes.

ça laisse rêveur ! qui s'y colle ?

Pour l'instant je fais mon problème tranquillement puis j'essayerais ^^

y aurait-il une appellation pour ces différents calculs? parce que pour la rédaction ce n'est pas toujours évident

pourrais-tu me corriger s'il te plait (au cas où )
les médianes : AA'=12 BB'=15 CC'=18

Aire (ABC) = 4/3 Aire (DEF) -> Héron
Aire (ABC) ≈119.06cm²

Périmètre:
j'ai fais la conjecture, mais problème :

Après avoir utilisé le théorème des médianes (puis multiplié les longueur par 2 comme j'ai dis hier a 18h45)
je trouve BC≈14.56cm AB≈9.486cm AC≈12.569cm

je vérifie avec Héron: la valeur est trop faible . Puis, si je multiplie par 4/3 puis par 3/2 j'ai ≈117.86cm²

re.

les longueurs de ABC sont :
20,59
17,78
13,56
son aire est bien 119,06.

vérifie tes calculs.

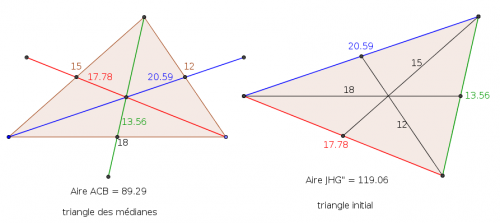
$fichier math$

désolé je viens de comprendre la méthode, mais il n'y a pas de nom de théorème ou autre pour dire que les coté de ABC = 3/4 de JHG?

moi je t'ai donné les longueurs de ABC (je n'ai pas très envie ni le temps de faire les calculs). je te suggère de procéder avec l'autre approche, que j'ai indiquée le 12.04.2010, à 17:44.

il n'y a pas d'autre solution que celle que je donne pour les côtés du triangle initial (valeurs approchées) :

20,59 cm -- 17,78 cm -- 13,56 cm.

attention : dans la figure, j'ai bêtement marqué Aire ACB = 89.29. ce n'est pas le "ABC" qui t'intéresse ; la réponse est la figure de droite (Aire JHG" = 119.06) - ce sont les notations du logiciel de GeoGebra que je n'ai pas modifiées.

m²_A = b²/2 + c²/2 - a²/4

c'est avec m milieu de A ?

non, c'est la médiane issue de A.