Construire un triangle connaissant ses médianes
-
Zauctore dernière édition par

Bonjour
Tout est dans le titre !
Étant données les longueurs m, n, p des trois médianes d'un triangle, comment le construire ?
C'est-à-dire, trouver ABC dont les médianes mesurent par exemple m=3, n=5 et p=7.
Dans une autre discussion, j'ai donné cette solution :
les côtés du triangle sont les 4/3 des médianes du triangle formé avec les médianes m, n et p.
(je ne l'ai pas inventé, c'est connu depuis au moins le dernier tiers du XIXe s.)En connaissez-vous d'autres ?
Qui s'y colle ?
Dans l'attente de vous lire...
-
Zauctore dernière édition par

Ou encore, comment disposer ces bouts de spaghetti :
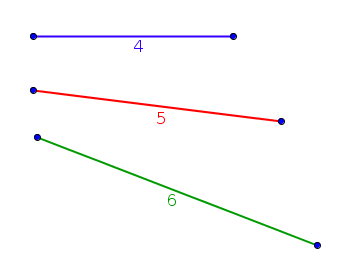
pour qu'un triangle les admette comme médianes ? comme ceci :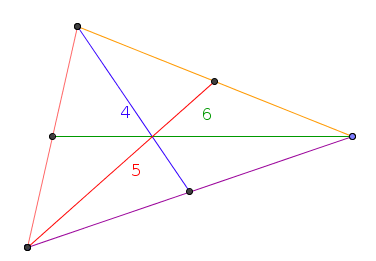
-
Salut,
Zauctore*les côtés du triangle sont les 4/3 des médianes du triangle formé avec les médianes.*Qu'est-ce que cela signifie ? Quand tu connais les longueurs des médianes, tu les multiplies par 4/3 et tu obtiens les longueurs du triangle correspondant ?
Et donc l'énigme que tu proposes consiste à construire le triangle connaissant la longueur de ses médianes sans avoir recours à cette propriété. C'est bien ça ?
-
Zauctore dernière édition par

nonon tu as mal lu : ce ne sont pas les médianes initialement données qu'il faut multiplier par 4/3 (si c'était si simple...
 ).
).j'ai donné un procédé - c'est surtout le défi de prouver sa validité qui vaut le coup !
et j'aimerais qu'on me signale une autre méthode...
-
Ok j'ai compris (je crois).
On a 3 longueurs de médianes, qui deviennent les côté d'un triangle. Et on multiplie les longueurs des médianes de ce dernier triangle par 4/3 pour obtenir les longueurs des côtés du triangle recherché.C'est une vraie question que tu poses, ou une énigme dont tu connais la réponse ?
-
Zauctore dernière édition par

t'as pigé

la preuve à retrouver (une fois que tu t'es persuadé que la méthode "marche" ... GeoGebra GeoGebra), ça c'est déjà un sacré défi dont je connais depuis peu le principe : c'est donc une "curiosité".
maintenant, la vraie question est de fournir d'autres méthodes s'il en existe : ça c'est une "énigme".
-
NNoé dernière édition par
Une méthode géométrique (je vous laisse la preuve
 ) :
) :
On veut construire un triangle ABC dont les médianes issues de A, B, et C, valent respectivement m, n et p.
On trace un segment [AA'] quelconque de longueur m (la première médiane). On place les points I et G sur ce segment tels que AI=IG=GA'=AA'/3.
On trace un cercle de centre I et de rayon n/3, et un cercle de centre G et de rayon p/3. On appelle C' une de leurs intersections (c'est le pied de la médiane issue de C).
On place B sur la demi-droite [AC') tel que AB=2AC'.
On place C sur la demi-droite [C'G) tel que C'C=p.
Et voilà !On peut même de cette façon construire le triangle à la règle et au compas, à condition bien sûr de savoir diviser une longueur par 3 à la règle et au compas, mais ça c'est facile.