Exercices sur le Produit Scalaire

Bonjour j'aurais besoin d'un petit peu d'aide si c'est possible.
J'ai deux exercices sur les produits scalaires et je bloque sur certaines questions:

Exercice1:

Le cercle C de centre O et de rayon 3 a pour diamètre [AB]. H est le point du segment [AO] défini par AH=2 et d est la droite passant par H est perpendiculaire à (AB). M est un point libre du cercle. La droite d coupe le cercle c en R et S, et la droite (AM) en L.

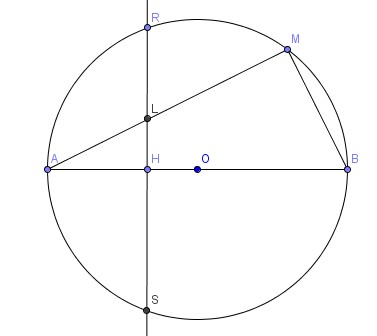
$fichier math$

Calculer le produit scalaire vecteurAL . vecteurAB et trouver trois autre produit scalaire qui lui sont égaux.

-> Selon moi vecteurAL . vecteurAB = vecteurAH . vecteurAB
=2×6×cos0
=12

vecteurAL . vecteurAB = vecteurAH . vecteurAB
vecteurAL . vecteurAB = vecteurAL . vecteurAM
vecteurAL . vecteurAB = vecteurAR . vecteurAB

Calculer le produit AL×AM

->Si LH = 1 (là est mon problème comment démontrer que LH=1 ?)
On a AL = √5 par Pythagore
Puis par Thales on a AL÷AM = AO ÷ AB
AM= (AL×AB)÷ AO
AM≈4,47

AL× AM ≈ 10

Déterminer la longueur AR. (Je bloque sur cette question.)

Exercice 2:

ABCD est un carré de côté a et de centre O. Les points I et J sont les milieux respectifs des segments [AB] et [AC].

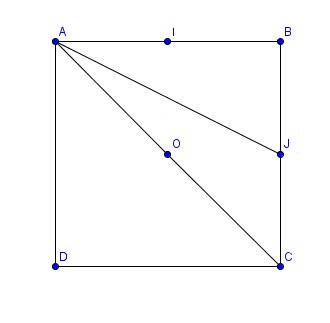
$fichier math$

Calculer les produits scalaires vecteurAI . vecteurAJ et vecteurAO . vecteurCD en fonction de a.

-> vecteurAI . vecteurAJ = vecteurAI . vecteurAB
= (a÷2) × a × cos45

vecteurAO . vecteurCD = vecteurAO . vecteur(-AB)
= (√(a²+a²)÷2) × (-a) × cos45

2)Calculer les distances AJ et AC en fonction de a

-> Par Pythagore:

AC²= AB²+BC²
AC= √(a²+a²)

AJ²=AB² + (BC÷2)²
AJ= √ (a² + (a÷2)²)

Montrer que vecteurAJ . vecteurAC = 3a²÷2 et déterminer l'angle JAC (De même je suis bloquer à cette questions)

Merci d'avance de l'aide que vous pourriez m'apporter.

non (premier exo presque faux)
AL.AB = AH.AB = 12

AL.AB = AH.AB = AS.AB = AR.AB

2)maintenant le produit AL*AM ici on a la multiplication de deux normes soit
ll AL ll * ll AM ll ce qui est aussi équivalent au produit scalaire AL.AM
puiske AL.AM = ll AL ll * ll AM ll * cos (0) (et cos 0 = 1)

pour calculer le produit scalaire on peut faire AL.(AB+BM)
ce qui donne AL.AB +AL.BM = 12 (puisque AL.BM = 0 )

donc AL*AM = 12

je continu l'exo ?

pour déterminer AR on peut utiliser un repere avec O le centre donc

A(-3;0) B(3;0) R (-1 ; y)

ici y= HR hors HR² = RO² - OH² (pythagore, RO (le rayon))

donc HR²= 9 - 1 = 8 HR=2√2 >>>> R(-1;2√2)

on cherche maintenant norme du vecteur AR (2;2√2)

√( 2² + (2√2)² ) = √ 12 = 2√3
AR=2√3

ou sinon sans repere on dit que AR.BR=0
(AH+HR).(BH+HR)= AH.BH + AH.HR + HR.BH + HR²
AH.HR=0 et HR.BH=0 ll AH ll =2 et ll BH ll = 4 (deux vecteurs sens opposé) donc AH.BH= -8
on a -8 + HR² = 0 ce qui donne bien HR²=8 et HR= 2√2

maintenant on fait pithagore puisqu'on connait deux normes AH et HR (on a pas utilisé de repere pour déterminer RH) (choisi la méthode qui te semble plus proche de ta lecon (produit scal)

Il me semble que c'est ce que j'ai mis pour AL.AB = AH.AB
mais j'ai penser que AM était le projeté de AB sur AL ?
merci
je pense qu'il faut faire avec pythadore mais mon problème est qu'il me manque des mesures ? (RH , RB)

désolé je n'avais pas vu ta dernière réponse ...

merci beaucoup !

euh j'ai remodifié mon message sur le calcul de RH (deux facons de faire)

je fais l'autre exo:

AI.AJ

B projeté ortho de J sur (AI)

AI.AJ=AI.AB

AB=a AI= a/2 donc AI.AB= a²/2

AO.CD

deux vecteurs sens opposé donc résultat négatif

on est dans un carré: 1) la diagonal d'un carré de coté a vaut a√2
AO=AC/2 donc AO=a√2/2

l'angle AC;AD = 45° = pi/4 et cos(pi/4) = √2/2

et CD= a donc AO.CD= a√2/2 * √2/2 * a= 2a²/4 = -(a²/2)

pour les distances

j'ai cité plus haut une propriété du carré mais je refais la démo
AC²= a²+a²=2a² AC=a√2

AJ²= AB²+BJ²
BJ=a/2 >> AJ²= a²+a²/4= 5a²/4
AJ= a(√5)/2

Merci effectivement je comprends mieux la deuxième.

regarde en bas j'ai fait la question 2 (tu veux que je fais la 3 aussi ??)

d'accord j'en fais un bout c tout simple regarde

AJ.AC = (AB+BJ).(AB+BC)
= AB² + AB.BC + BJ.AB+ BJ.BC

AB.BJ=0 et AB.BC=0

AB²=a² et
BJ.BC= a/2*a
= a²/2

donc on a
a² + a²/2
= 2a²/2 + a²/2
= 3a²/2

voila (je fais aussi la derniere question qui en faite utilise la definition produit scalaire avec cosinus ... ????)

J'ai compris mes erreurs mais c'est surtout sur la 3 que je bloquais donc je veux bien un peu d'aide si ça te gène pas ?

...

une piste ( AJ.AC = ll AJ ll * ll AC ll * cos (AJ;AC) = 3a²/2 (ce qu'on a prouvé) )

donc en remplassant avec les valeurs (qu'on a également calculer a la question 2 on trouve ...???)

je continue , ou t'es toujours bloqué?

a√5/2×a√2×cos(AJ;AC) = 3a²/2
On est d'accord mais c'est juste dans les calcul que je trouve quelque chose d'improbable 6a²/(2a√5×2a√2)

lol non regarde

a√2 x a√5/2 x cos (AJ;AC) = 3a² / 2

a²√10/2 x cos (AJ;AC) = 3a² / 2

(3a²/2)/(a²√10/2) = cos (AJ;AC)

(3a²/2) x (2/a²√10) = (3/√10) = cos (AJ;AC) environ 18 °

MERCI BEAUCOUP