statistique, boites de dispersions

a l' aideeee je bloque sur la premiere question, il faut faire comment?

Exercice 2
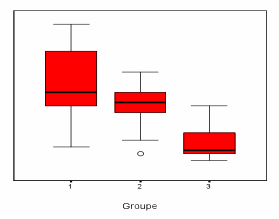
Afin d'étudier les effets de trois thérapies différentes sur la prise de poids chez des jeunes filles traitées pour l'anorexie, on a constitué trois groupes contenant respectivement de 30, 25 et 20 jeunes filles. Au bout d‘un certain temps de traitement, on a mesuré la prise de poids. A partir des observations, on a construit les boîtes de dispersion

**1) Les moyennes des groupes rangées par ordre croissant sont égales à 0,45 4,01 7,56 et les trois variances rangées par ordre croissant sont égales à 7,156 13,556 32,091

Sans calcul et en justifiant votre réponse, attribuer à chacun des groupes sa moyenne et sa variance.**
2) Calculer l'écart-type dans chacun des groupes
3) Dire pour chacun des groupes si la médiane est inférieure, égale ou supérieure à la moyenne.
4) Que se passerait-il sur la valeur de la médiane, des quartiles, de la moyenne et de l'écart-type du groupe 2, si on ramenait la valeur extrême du groupe 2 à l'intérieur de la moustache ?
5) Calculer la moyenne de l'ensemble des 75 jeunes filles.
6) Comparez l'effet des différentes thérapies

MERCIIII BCP!

boite de dispersion

Bonjour,

A partir de l'indication de la médiane, tu dois pouvoir placer les moyennes. La variance, et l'écart type te donne l'indication de l'écart par rapport à la moyenne.

Indique tes éléments de réponse.

bonjour!! merci de la reponse!

donc ca pourrais etre, tout simplement:

groupe 1: 7.56
groupe 2: 4.01
groupe 3:0.45
grace a l'emplacement de la mediane sur le graphique

et la variance

groupe 1:32.091
groupe 2: 12.556
groupe 3: 7.156

en regandant les moustaches.

c'est ca?
ou j'ai rien compris

C'est faux.

Si j'analyse le premier diagramme, la médiane se situe en dessous de 5, cela indique qu'il y a autant de valeurs inférieures à 5 que de valeur supérieures à 5.
De plus 1/4 des notes sont comprises entre environ 4 et 5 et 5 et 7.
Donc ....

donc
groupe 1: moyenne:4.01 et variance 7.156??

comment je vois que la mediane se situe en dessous de 5?

La médiane correspond au trait noir placé dans le rectangle rouge.
A partir de la variance, calcule l'écart type puis moyenne - écart type ; moyenne + écart type.

ecart type est √7.156=2.675

mais apres je sais vraiment pas comment faire,comment a partir de l'ecart type on arrive a identifier la moyenne?
:frowning2:

C'est à partir de la médiane est des quartiles Q1 et Q3 que tu situes la moyenne.
Pour le dernier diagramme plus de 50% des résultats sont inférieurs à 5, et la médiane est voisine de 2, donc la moyenne est 0,45
Si je choisis √32,091 = 5,66
0,45 -5,66 = - 5,21
et
5,66 +0,45 = 6,11
Cela indique qu'une majorité des valeurs est comprise entre 0 et 6,11
Si je choisis √13,556= 3,68
0,45 - 3,68 = -3,23
0,45+3,68 = 4,13
Cela indique qu'une majorité des valeurs est comprise entre 0 et 4,13

Fais le troisième cas et détermine lequel est le bon.

√7.156=2.675
0.45-2.675=-2.225

0.45+2.675=3.125
valeurs comprise entre 0 et 3.125
donc pour la moyenne 0.45 la variance est 7.156 ou 13.556

surement pas 32.091 car les valeurs sont plus elevee de 5?
c'est ca?

dsl.... je comprend pas

et donc quand il nous demande de le determiner que a partir du graphique on peut pas?

je desespere!

Tu peux avec les graphiques.
L'analyse de la médiane et des quartiles te permet de situer la moyenne que tu positionnes sur le graphique.
Ensuite tu compares les écarts de la moyenne par rapport aux quartiles avec les variances.

Tu n'as pas une échelle sur le dessin des boites ?

Ton résultat sur les moyennes est correct. Il te reste à attribuer les variances.

non... aucune echelle!

donc pour le groupe 1:7.56 et la variance
√32.091=5.66
7.56-5.66=1.9
7.56+5.66=13.22

donc il me semble que ca soit groupe 1 m=7.56 et v 32.091

pour le groupe 2:4.01 et la variance

√7.156=2.675
4.01-2.675=1.33
4.01+2.675=6.685

et pour le groupe 3:0.45 et la variance

√13.550=3.68
0.45-3.68=-3.23
0.45+3.68=4.13
donc entre 0 et 4.13

je suis sure que ca soit ca!!

ou je me trompe encore?

Oui c'est correct, pour la variance, il suffit de comparer les hauteurs.

Pour le dernier :
0.45-3.68=-3.23
0.45+3.68=4.13
donc entre -3,23 et 4.13 puisque le 0 est indiqué sur le schéma.

mais le 0 n'est pas indique.. sur le groupe 2 tu dit?

c'est une valeur extreme, non?

n'empeche MERCI MERCI et ENCORE MERCI BEAUCOUP!!!