Donner le barycentre de trois points pondérés
-
Rrasha dernière édition par Hind
Bonjour,
j'ai un DM , je l'ai presque terminé seulement je bloque sur un exercice, voila l'énoncé :
ABC est un triangle rectangle en A. I est le milieu de [BC], Γ est le cercle de centre A passant par I. G est le point de Γ diamétralement opposé à I.- Prouver que le point G est le barycentre de (A;4), (B;-1), (C;-1)
- Trouver deux réels a et b tels que A est le barycentre de (G;2), (B;b), (C;a)
- Quel est l'ensemble des points M du plan tels que: ||2MG+MB+MC||=2||BC|| ? (ce sont des vecteurs)
J'ai essayé de le faire mais je ne comprends pas du tout.
Je vois pas du tout comment m'y prendre, si quelqun pouvait m'éclairer...Merci d'avance !!
-
Zauctore dernière édition par

salut et bienvenue ici
avant de t'attaquer à ce genre d'exo, sois bien au fait des définitions et propriétés de base (placement, associativité) des barycentres
voici déjà la figure :
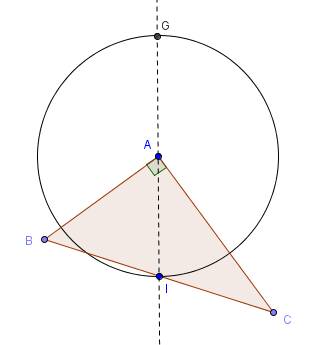
Pour la question 1, tu peux commencer par remarquer que le barycentre de (B,-1) et (C,-1) est un point déjà placé sur la figure ! appelons-le *temporairement *F.
Il suffira alors de montrer que G est le barycentre de (A,4) et (F,-2), - c'est-à-dire de ce (A,2) et (F,-1), qui est ... presque évident.Pour la 2e question, A étant le milieu de [GI], c'est le barycentre de (G,1) et (I,1) - ou de (G,2) et (I,2).
Or, I est lui-même le barycentre de (B,1) et (C,1) pour la même raison.
-
Rrasha dernière édition par
non je ne comprends pas ce que tu as fait, j'ai compris la figure , pour F(c'est-à-dire C, c'est ce que tu as dit) j'ai compris mais comment je fais pour démontrer que G est barycentre de (A,2), (F,-2).
j'ai completement oublié...