Problème d'angles dans un triangle

Bonjour !

Tout d'abord, merci d'avance de l'aide que vous voudrez bien m'apporter !
Il s'agit d'un problème d'angles posé en "défi" sur le Transmath 5ème 2006 ( N°82 p 175
Comme j'ai la figure sous les yeux, je vais essayer de vous la décrire :
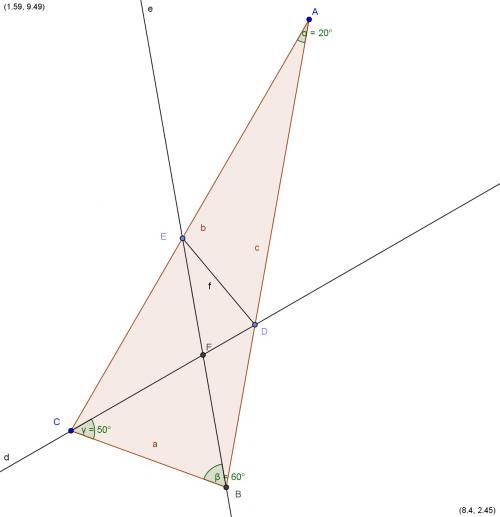
J'ai un triangle ABC isocèle en A dont l'angle au sommet principal A est de 20°.
J'ai une demi-droite d'origine B qui fait un angle de 60° avec (BC) et qui coupe le côté AC en E ; j'ai aussi une demi-droite d'origine C qui fait un angle de 50° avec (BC) et qui coupe le côté AB en D ; ces deux demi-droite se coupent en F. La question posée est : "calculer les angles du triangle DEF" ! Je suis arrivé à calculer l'angle F ( 70° ) et faisant une figure précise avec mes instruments, je remarque que les angles D et E font exactement 80° et 30° mais je n'arrive pas à les calculer !
Pourriez-vous m'indiquer un chemin à suivre ? Apparemment, comme on doit utiliser Angles; Triangles et Parallèlisme, il doit y avoir un calcul simple mais je ne vois pas...

Merci pour votre aide !

Bonjour,
Je veux bien t'aider mais je ne comprends pas ton problème que cherche tu ?

Bonjour,

Hé bien, je cherche à CALCULER la valeur des angles D et E du triangle DEF ( j'ai déjà calculé la valeur de l'angle F qui est de 70° ... ). Comme je n'arrive pas à calculer ces 2 angles D et E, j'ai fait une figure très précise avec ma règle et mon rapporteur et lorsque je mesure F, il fait bien 70° ( donc mon calcul est juste ) et lorsque je MESURE les angles D et E, ils font respectivement et très précisément 80° et 30° mais je n'arrive pas à trouver une preuve par le CALCUL de la valeur de ces 2 angles !! J'ai essayé de tracer la parallèle à (BC) passant par D puis appliquer les règles d'angles et parallélisme ou de tracer la parallèle à (BC) passant par E... mais je tourne en rond... je n'arrive pas à trouver une relation entre tous ces angles... c'est pas facile !

Peux-tu m'aider, STP ? Merci d'avance !

Bonjour !

Je rame toujours autant ! Toutes mes recherches n'aboutissent à rien ! Personne n'a une idée ou un début de démo ?

Merci.

salut

n'ayant pas trop le courage de chercher à déchiffrer cette consigne... ce n'est pas bien, je sais ... je te demande s'il ne te serait pas possible de dessiner un schéma du problème (avec Paint par exemple), image que tu hébergerais ici (bouton Ajoute une image ci-dessous).

merci

Bonjour,

J’avais jeté un œil à ton exo la semaine dernière, mais . . .

$fichier math$

^EFD = 70° est juste.

En utilisant le fait que le triangle ABC est isocèle en A (les angles à la base sont de même mesure), on déduit les angles ^ABC et ^ACB

Puis en utilisant la somme des angles est égale à 180° dans chacun des triangles , on obtient plein d'angles ... mais pas ceux recherchés apparemment : ^DEF et ^EDF si j’ai bien compris.

On a juste ^DEF + ^EDF = 110°

En utilisant ^BCD et ^CDB on peut montrer que BCD est isocèle en B, je ne sais pas si c'est utile.

Mais la méthode pour aboutir aux calculs de ces deux angles m’échappe . . . faut que je refasse une 5ème !

Salut à tous !

Merci des réponses que vous m'avez données ! Je pense de plus en plus qu'il manque une donnée dans ce problème de "défi" de 5ème car sinon, au bout du compte, on aurait trouvé la solution ! J'ai le père d'un ami qui l'a fait avec de la "géométrie analytique" mais la formule est dure, ya des "tangentes" quelque chose mais apparemment, vu les données, c'est faisable ! Bon, encore un mystère non résolu...

Thanks à tous

Nat