DM sur les fonctions symetrie et équations

je suis en première S et jai vraiment besoin d'aide pour la partie B de mon DM S'IL VOUS PLAIT!!!!! :rolling_eyes: :rolling_eyes: :rolling_eyes:
Voici le sujet :

Soit ABCD un rectangle tel que AB=1 et AD=2. Soit I le milieu du segment [AB] et M un point du segment [D]. on pose AM=x.

Soit J l'ensemble des valeurs que peut prendre x. Déterminer J.
On pose f(x)= MI²+MC².
a. pour tout x élément de J, exprimer f(x) en fonction de x.
b. Vérifier que : pour tout x élément de J, g(x)=4f(x).
c. En déduire le tableau de variation de f sur J.
on note Cf la courbe représentative de la fonction f dans un repère orthogonal. (unité sur l'axe : 4cm en abscisse et 2 cm en ordonnées)
a. démontrer que la droite delta d'equation x=1 est un axe de symétrie de Cf.
b. tracer Cf.
On se propose de determiner les valeurs de x pour lesquelles le triangle IMC est rectangle en M.
a. Montrer qu'un point M répond à la question si et seulmen si f(x) = $174\frac{17}{4}$
.
b. resoudre graphiquement l'équation f(x)= $174\frac{17}{4}$
c. Resoudre graphiquement l'équation f(x) = $174\frac{17}{4}$
par le calcul

Aider moi en me donnant ce que vous pouvez !!!! je suis vraiment desespéree alors mercii de vortre aide d'avance!!!

jai vraiment besoin d'aide surtout pour la question 2.b et la 4.a s'il vous plait !

Bonjour hélène,

Tu as fait un schéma ?

M ∈ [AD] . . . or AD = 2 . . . et AM = x

donc quelle est la valeur mini que peut prendre x ?
et la valeur max ?

2a) Utilise Pythagore dans les triangles AIM et MCD

Bonjour! merci de repondre !!

enfaite jai fait un schema mais après je suis vraiment bloquée!
pour la 1) je dirai que la valeur min de x est 0 et la max est 2 ?!!

et la 2) jai pa compri comment jdoi utilisé pythagore, je vois que MI et MC sont les hypoténuse mais apres je suis vraiment perdu :s

On a ceci :

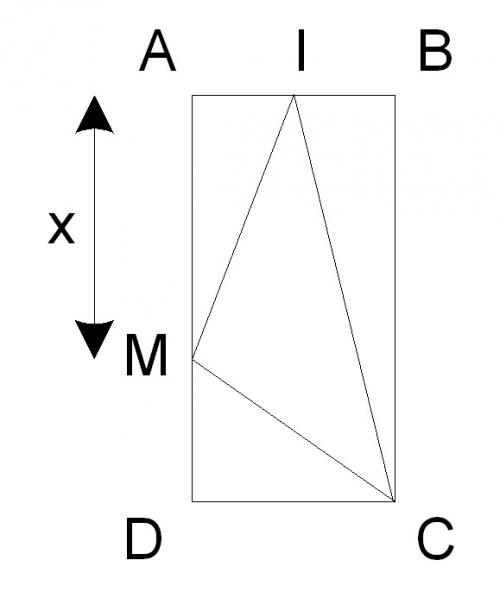
$fichier math$

Citation
enfaite jai fait un schema mais après je suis vraiment bloquée!
pour la 1) je dirai que la valeur min de x est 0 et la max est 2 ?!!

Oui J = [0;2]

Citation
et la 2) jai pa compri comment jdoi utilisé pythagore, je vois que MI et MC sont les hypoténuse mais apres je suis vraiment perdu :s

Dans le triangle AIM rectangle en A : le th de Pythagore
MI² = AI² + AM²

avec AI = 1/2 et AM = x tu calcules MI² en fonction de x

puis idem dans l'autre triangle.

oui c'est bien un schema comme lui que j'ai obtenue ! pour 2.a) jai obtenue
f(x)= $12\frac{1}{2}$ + $32\frac{3}{2}$ x+x².

merci jai compris pour cette question et pour le reste je dois faire comment svp ?

Je vais devoir quitter ... alors la méthode :

2a) Pythagore nous donne MI² = x² + 1/4 et MC² = x² - 4x + 5

j'obtiens de mon coté f(x) = 2x² - 4x + 21/4

2b) si c'est moi qui ait bon alors g que tu n'as pas donné dans ton texte doit être g(x) = 8x² - 16x + 21
est-ce bien ça ?

2c) f = (1/4) g

f est donc de la forme k×g avec k positif. Tu en déduis le sens de variation de f par rapport à celui de g (je suppose que tu as étudié g dans une première partie)

3a) la droite x=a est un axe de symétrie si pour tout h réel f(a-h) = f(a+h)

tu appliques ici avec a=1

4a) IMC est rectangle en M ssi IC²= ... (Pythagore dans IMC)
tu reconnais f(x) dans cette égalité

Pour obtenir IC², à nouveau Pythagore dans IBC

4c) C'est une équation du second degré à résoudre. Je suis sûr que tu sais faire

pour vérifier tes résultats, je trouve de mon coté : $2−22\frac{2-\sqrt{2}}{2}$ et $2+22\frac{2+\sqrt{2}}{2}$

J'espère qu'une autre pers prendra la main pour la suite ... N'hésite pas à faire appel aux bonnes volontés.

Merciiiii beaucoup de m'avoir aider, depuis que je suis en première je me sens souvent perdu en maths! je vais refaire les calculs de mon coté et puis je vous tiendrais au courant! merci encore!

Iron
3a) la droite x=a est un axe de symétrie si pour tout h réel f(a-h) = f(a+h)

tu appliques ici avec a=1
Il est probable que tu n’aies pas encore vu cette méthode. Tu peux peut-être utiliser le fait qu’il s’agit d’une parabole tournée vers le haut de sommet S dont tu détermines les coordonnées. La droite d’équation y = $x_S$ est alors un axe de symétrie de la parabole.

oui j'ai vu en cours la propriété sur la symetrie!
Et enfaite ds la partie A jai bien eu g(x)= 8x²-16x+21
jai du le mettre sous forme canonique, trouver ses variations et resoudre g(x)=0 et g(x)=17.

sinon pour la question 4a) jai trouvé IC²=2x²-4x+ $214\frac{21}{4}$ dans le triangle IMC et IC²= $94\frac{9}{4}$
dans le triangle IBC donc jvois pas le rapport avec le $174\frac{17}{4}$
du sujet !?

hélène16
pour la question 4a) jai trouvé IC²=2x²-4x+ $214\frac{21}{4}$ dans le triangle IMC et IC²= $94\frac{9}{4}$
dans le triangle IBC donc jvois pas le rapport avec le $174\frac{17}{4}$
du sujet !?
IC² n'est pas correct : triangle IBC rect en B et IC²= IB² + BC² = (1/2)² + 2² = ...

combien tu trouves ?

édit : correction triangle IBC

hélène16
4a) jai trouvé IC² =
2x²-4x+ (21/4)
As-tu reconnu l'expression en bleu ?

ah oui jai obtenue IC²= $174\frac{17}{4}$ dans le triangle IBC.

et IC²=2x²-4x+ $214\frac{21}{4}$
dans le triangle IMC (sachant qu'on a calculé MI² et MC² dans la question 2a).

et donc IC²= 2x²-4x+ $214\frac{21}{4}$ = $174\frac{17}{4}$ = f(x)

ensuite jai di que M répond ainsi à la question

Le triangle IMC sera rectangle en M pour les valeurs de x telles que f(x) = 17/4

avec x = AM ne l'oublions pas

Ah oui!!
Merciiiiiii beaucoup pour cette aide!!

C'est vraiment gentil de m'avoir aider parce que avant j'avais pas compris pas mal de choses dans le DM!!

A bientôt peut-être

Je t'en prie

Bon we et à la prochaine

N'oublie pas de travailler dans / de préciser l'ensemble de définition de f (déterminé en question 1) pour les autres questions 2c) 3a) 4c) vérifier que les solutions trouvées appartiennent bien à Df (x ne peut pas prendre n'importe quelle valeur)

euh pour la question j'ai juste mi que J=[0;2] car M appartient a [AD] et AM=x, donc l'ensemble de définiton de x?? je sais pas si mes résultats le vérifient

2c) jai mi -1 pour x et $−134-\frac{13}{4}$
pour f(x) (dans le tableau de variations)

3a) jai démontré avec la propriété de mon cours f(a-h) (a+h) avec a-h et a+h =1 jai trouvé 0

4c) jai trouvé le meme résultat que vous

Bonjour,

Ce que je voulais dire, c'est qu'il faut limiter le tableau de variation de f à son ensemble de définition Df = J = [0;2]

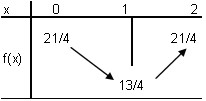
$fichier math$

En fin d'exo, vérifier que les solutions trouvées $2−22\frac{2-\sqrt{2}}{2}$ ≈ 0,29 et $2+22\frac{2+\sqrt{2}}{2}$ ≈ 1,71 appartiennent bien à Df = J

Les petits détails (rigueur) qui font la différence entre la bonne note et la très bonne note.

Citation
3a) jai démontré avec la propriété de mon cours f(a-h) (a+h) avec a-h et a+h =1 jai trouvé 0
Je n'ai pas bien compris ta phrase ... je suppose que tu as calculé f(1-h)-f(1+h) pour trouver zéro.

ok!! Merciii