Lieu Géométrique.

Bonjour à tous, j'ai un très gros problème avec un exercice de Math, et je bloque complètement...
Voici l'énoncé:

Soit f la fonction définie, pour tout réel x ≠ 1, par :
f(x) = x^3 / (x-1)²
Et C sa courbe représentative dans le plan muni d’un repère orthogonal (O, i, j).
1°) Etudier les variations de la fonction f
2°) Déterminer des réels a, b, c et d tels que, pour tous réel x ≠ 1 :
f(x) = ax + b + [ (cx + d) / (x – 1)² ]
En déduire la position de la courbe C par rapport à la droite D d’équation y = x + 2.
3°) Déterminer l’abscisse du point J de la courbe C en lequel la tangente est parallèle à la droite D, puis une équation de cette tangente T.
4°) Tracer la courbe C et les droites D et T.
5°) a) A l’aide graphique, étudier, suivant les valeurs du paramètre p, le nombre de solution de l’équation : f(x) = x + p.
b) Préciser l’ensemble D des valeurs de p pour lesquelles cette équation admet deux solutions distinctes.
6°) Lorsque la droite Δ d’équation y = x + p coupe la courbe C en deux points M et N, on note P le milieu le milieu de [MN].
On s’intéresse au lieu géométrique du point P.
a) Démontrer que les abscisses des points d’intersection M et N sont les solutions de l’équation (E) (p-2)x² + (1-2p)x + p = 0.
b) En déduire que l’abscisse du point P est :
xP = 1 + [ 3 / (2p – 4) ]
et démontrer que P appartient à la courbe C d’équation :
y = x + 2 + [ 3 / 2(x – 1) ]
c) Quel est l’ensemble décrit par xP lorsque p décrit D ?
d) Etudier les variations de la fonction g définie, pour tout réel x ≠ 1, par :
g(x) = x + 2 + [ 3 / 2(x – 1) ]
et tracer la courbe C’.
Préciser la partie de la courbe C’ décrite par le point P lorsque la droite Δ prend toutes les positions possibles.

Voici mes réponses:

1°) Pour cette question, j'ai tout d'abord calculé la dérivé de la fonction.
Je trouve f'(x) = [ x² (x² - 4x + 3) ] / [ (x-1)^4 ]
Puis, j'étudie le signe. On sait que (x-1)^4 est toujours positif, il s'annule pour la valeur x = 1 et que x²(x²-4x+3) avec x² étant aussi toujours positif donc il suffit d'étudier la fonction polynôme. On calcul le discriminant et on trouve deux solutions: x=3 et x=1.
Ainsi, on peut dresser le tableau de variation suivant :

http://www.weplug.com/images_1/6133c84fdba678f4532a2d94a7ed55c220100918050900.jpg

Mais pour le reste, je bloque complètement..
Merci d'avance pour votre aide et vos conseils!

Bonjour

Citation
f(x) = x^3 / (x-1)²

2°) Déterminer des réels a, b, c et d tels que, pour tous réel x ≠ 1 :
f(x) = ax + b + [ (cx + d) / (x – 1)² ]

En déduire la position de la courbe C par rapport à la droite D d’équation y = x + 2.

Alors ici rends-toi compte que le problème revient à trouver a, b, c et d tels que pour x différent de 1 on ait

(ax + b)(x-1)² + (cx + d) = x³.

Merci beaucoup!
Donc pour la 2°) Je trouve bien a=1, b=2, c=3 et d=-2.
on peut donc ensuite faire f(x) - (x+2) et on trouve (3x-2)/(x-1)².
Donc en +infi, la courbe représentative de f et la droite d'équation y = x+2 tendent à se rapprocher indéfiniment, donc que la droite d'équation y = x+2 est une asymptote oblique à la courbe représentative de f . Correct ?

Pour la 3°), en posant f'(x)=1, je trouve x= 1/3.
Donc j'en ai déduis que l'équation de la tangente est y = x - 1/4.

Ensuite, pour la question 4°), voici le lien :

http://www.wepl...18174605.png

Pour la 5°) a), je n'ai pas vraiment compris le but de la question et ce qu'on doit chercher. Qu'est-ce que le paramètre p ?

Merci.

Re.

Alors pour f(x) = x+p c'est le nombre infini d'équations

f(x) = 0
f(x) = 1
f(x) = 2
etc.

qu'il te faut résoudre à chaque fois si je puis dire, sans compter tous les autres coefficients comme -5 ou 4/3 ou $p i$ etc.

Géométriquement, ce sont les droites "obliques" parallèles à la droite y=x, tu peux t'en servir pour indiquer en combien de points elles recoupent la courbe.

Je ne suis pas sûr du tout d'avoir compris.. Mais en regardant mon graphique, je vois que la courbe y=f(x) et la droite y=x+p se coupe en un seul point.. Non, en faite c'est y=x+2.. Mais je ne vois pas du tout à quoi correspond la droite y=x+p ...

Re.

C'est une famille de droites (p est un paramètre qui peut prendre n'importe quelle valeur, et à chacune de ces valeurs, est associée une et une seule droite, parallèle à y = x) : en voici quelques-unes.

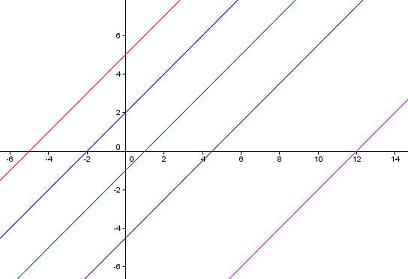
$fichier math$

Merci beaucoup.

Et pour la question 6°)c), qu'est-ce qu'ils entendent par "ensemble décrit par xP lorsque p décrit D" ?