Vecteur (I).

Bonjour! Quelqu'un peut-il m'aider, Juste me donner des pistes! Merci!

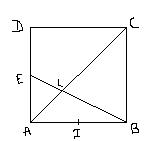
$fichier math$

Soit un carré ABCD, E le milieu de [AD], I le milieu de [AB], L le point d'intersection des droites [AC] et [BE].
On veut démontrer, avec plusieurs méthodes, que les points D, I, L sont alignés.

1ère méthode : Calcul analytique. On considère le repère (A; AB $→^\rightarrow$ , AD $→^\rightarrow$ ).

a) Donner les coordonnées des points A, B, C, D.

b) Calculer les coordonnées des points E et I.

c) Déterminer une équation des droites (AC) et (BE) puis calculer coordonnées du point L.

d) Montrer que les points D, I, L sont alignés.

2ème méthode : les propriétés du triangle.

a) Que représentent les droites (AC) et (BE) pour le triangle ABD? Justifier.

b) Montrer que les points D, I, L sont alignés.

Bonjour. Vois dans ton carré un repere, d'axe x AB→ et d'axe y le vecteur AD. Considere AB pour 1 unité, idem pour AD !

Oui, Merci, ça je l'ai déjà fait ^^

Tu en es ou alors?

Au c)

Ah et bien la je ne peux plus t'aider ! Je suis en Terminale ES, j'avais vu les premieres questions en Spe maths l'année derniere, et la je bloque ! Desole!

Ok! Merci!^^ C'est pas grave

Bonjour

Es-tu d'accord que (AC) : y = x et (BE) y = 1/2 - 1/2x ?

Rq : à l'avenir, précise ce que tu as fait, où tu en es, plutôt que de poster un simple énoncé brut ; merci.

Je ne comprend pas trop.. Peux-tu m'expliquer si ça ne te dérange pas ?

( Oui Désolée.. J'ai oublié de le préciser.. )

Bien

Voici une méthode:

les coordonnées de A dans le repère sont (0;0)
celles de C sont (1;1)
la droite y = ax + b qui passe par A et C vérifie 0 = a0+b et 1 = a1 + b.
d'où les valeurs de a et b, et l'équation de (AC) : y =x.

(on peut aussi remarquer que (AC) est la 1re bissectrice des axes, ce qui permet de donner son équation plus vite)

La méthodeque je viens de montrer fonctionne aussi pour (BE).

Ok; Merci beaucoup !