exercice sur nombre complexe

soit p(x)=zde puissance 4 -3z³ + 9/2z²-3z+1.
montrez que si z∈C est solution de l'équation E: p(z)=0alors conjuqué de z est egalement solution.
2: verifiez que 1+i est solution de E. puis en deduire que P(z) se factorise sous la forme de produit de 2 polynome a coefficiant reel. pui resoudre E.

sil vous plait aider moi je ne comprend pas la premiere question et la deuxieme. MERCI d'avance.

Bonsoir

Pour la première question, les coefficients ont entiers : tu peux donc prendre le conjugué de p(z) et l'application des règles sur le conjugué montrera que $p(z)‾=p(z‾)\overline{p(z)} = p(\overline{z})$ .

Ainsi si z est racine, alors p(z) = 0 impliquera que p(z barre) = 0 aussi.

si je comprend bien il faut que je calcule le conjugué de z pour la premiere question. est ca? pour la deuxieme je pense qu'il faut calculer p(1+i)=0 mais apres je ne comprend pas. pouvez m'expliquer?

Comme l'a indiqué Zauctore, pour la 1) tu calcules le conjugué de p(z) et tu aboutis progressivement à p(z barre) en utilisant les propriétés des conjugués :

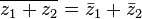
$http://upload.wikimedia.org/math/0/f/c/0fc3782c687d31eab93ffb46c1b8c7dd.png$

$http://upload.wikimedia.org/math/7/3/f/73f6f1d24d40475dea0a401b673f08f5.png$

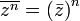$http://upload.wikimedia.org/math/e/7/8/e78db2eab8e001b9e532db36b6041e2b.png$ n∈ $mathbb{N}$

(extrait de wikiversité)

Pour la 2), tu calcules p(1+i)

p(1+i) = $1+i)^4$ - 3(1+i)³ + (9/2)(1+i)² - 3(1+i) + 1 = ...

tu devrais trouver 0

apres pour factoriser p je prend quoi alor?

Si 1+i est solution de p(z)=0 alors p(z) peut se factoriser sous la forme :

Edit : p(z) = [z-(1+i)] q(x)

ok merci

desole mais je n'y arrive pas.
Pour le premier, je vois pas comment on calcule le conjugue de z. faut il remplacer z par a+bi.
pour le 2 je ne trouve pas 0 avec 1+i mais je trouve p(1+i)=5-6i.
apres pour le factoriser q(x) est un polynome du second degre ou pas.

desole mais je n'y arrive pas.
Pour le premier, je vois pas comment on calcule le conjugue de z. faut il remplacer z par a+bi.
pour le 2 je ne trouve pas 0 avec 1+i mais je trouve p(1+i)=5-6i.
apres pour le factoriser q(x) est un polynome du second degre ou pas.

desole mais je n'y arrive pas.
Pour le premier, je vois pas comment on calcule le conjugue de z. faut il remplacer z par a+bi.
pour le 2 je ne trouve pas 0 avec 1+i mais je trouve p(1+i)=5-6i.
apres pour le factoriser q(x) est un polynome du second degre ou pas.

Iron
Si 1+i est solution de p(z)=0 alors p(z) peut se factoriser sous la forme :

p(z) = (1+i) q(x)

C'est parce que je me suis trompé, je rectifie :

Si 1+i est solution de p(z)=0 alors p(z) peut se factoriser sous la forme :

p(z) = [z-(1+i)] q(x)

Désolé !

paulo69
Pour le premier, je vois pas comment on calcule le conjugue de z. faut il remplacer z par a+bi
Non, il faut laisser z

donc pour le un je calcule le conjuque de p'z) mais je ny arive pas.

$p(z)ˉ=z4−3z3+92z2−3z+1ˉ=z4ˉ−3z3ˉ+92z2ˉ−3zˉ+1ˉ=...\bar{p(z)}=\bar{z^4 - 3z^3 + \frac{9}{2}z^2-3z+1} = \bar{z^4} - \bar{3z^3} + \bar{\frac{9}{2}z^2}-\bar{3z}+\bar{1} = ...$

mais comment on sait le conjugue de 9/2z² sest egal a conbien et els autres aussi?

Il faut utiliser les règles de calcul des conjugués :

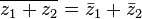
$http://upload.wikimedia.org/math/0/f/c/0fc3782c687d31eab93ffb46c1b8c7dd.png$

$http://upload.wikimedia.org/math/7/3/f/73f6f1d24d40475dea0a401b673f08f5.png$

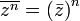$http://upload.wikimedia.org/math/e/7/8/e78db2eab8e001b9e532db36b6041e2b.png$ n∈ $mathbb{N}$

$p(z)ˉ=z4−3z3+92z2−3z+1ˉ=z4ˉ−3z3ˉ+92z2ˉ−3zˉ+1ˉ=zˉ4−3ˉz3ˉ+(92)ˉz2ˉ−3ˉzˉ+1ˉ=zˉ4−3zˉ3+92zˉ2−3zˉ+1=p(zˉ)\bar{p(z)}=\bar{z^4 - 3z^3 + \frac{9}{2}z^2-3z+1} = \bar{z^4} - \bar{3z^3} + \bar{\frac{9}{2}z^2}-\bar{3z}+\bar{1} = \bar{z}^4 - \bar{3}\bar{z^3} + \bar{(\frac{9}{2})}\bar{z^2}-\bar{3}\bar{z}+\bar{1} = \bar{z}^4 - 3\bar{z}^3 + \frac{9}{2}\bar{z}^2-3\bar{z}+1 = p(\bar{z})$

Vérifie que je ne me suis pas trompé avec tous ces "barres" en latex