Dresser le tableau de variation d'une fonction

Bonjour,
J'aurai besoin d'aide pour cet exercice qui me pose vraiment problème, si quelqu'un pouvais m'aider se serait très gentil

On considère la fonction f définie par f (x) = 624 - 6x - 2 400/x sur ] 0 ; + inf [
on pose g(x) = 624 - 6x et k(x) = -2400 / x sur ] 0 ; + inf [

1a. donner le sens de variation des fonctions g et k. justifier. Peut on en déduire le sens de variation de la fonction f? pourquoi?

2b. établir le tableau de variation de la fonction f. déduire les dimensions d'une page pour obtenir une surface imprimable maximale.

1c. calculer le pourcentage que représente cette aire maximale par rapport à l'aire totale d'une page.

Merci de votre aide

Bonjour,

Calcule la dérivée et étudie son signe.

Alors pour le calcul de la dérivée de f(x) j'ai trouvé :

f'(x) = -x + 2400 / x²

Je ne sais pas comment faire pour étudier son signe avec le tableau de variation?

Non,

La dérivée de -6x est -6

Et pour g et k ? question 1a.

alors c'est donc :
f'(x) = -6 + 2400 / x²
g'(x) = -6
k'(x) = 2400/x²
non?

C'est correct.

Et ensuite comment on peut en déduire le sens de variation?
A part la calculatrice je ne sais pas

Pour le sens de variation, tu étudies le signe de la dérivée.
g'(x) = -6, donc la fonction g est décroissante ou croissante ?

la fonction g est décroissante, f est croissante et k est croissante?

Pour g et k, c'est correct mais pas pour f.

Comment as-tu trouvé les variations de f ?

pour f je savais pas trop parce que y'a un x² et normalement c'est toujours positif on m'a dit.. mais apres y'a aussi -6

g étant décroissante et f croissante, donc pas la même variation, on ne peut pas conclure pour f.

Résous f'(x) = 0.

f (x) = 624 - 6x - 2 400/x
donc pour f'(x) = 0

f(x) = 624 - x -2400 /x soit -x + 624 = -2400 /x²
donc : ( 642 - x ) ( x² ) = -2400 ?

Je ne sais pas du tout faire pour résoudre f'(x) = 0 ?

Tu as écrit plus tôt : f'(x) = -6 + 2400 / x²,
il ne te reste donc qu'à résoudre -6 + 2400 / x² =0 ...

f'(x) = -6 +2400 / x²
donc :
f = 0 donne : -6 + 2400 / x²
soit : 6 - 2400 / x²

donc : 6x² = 2400

non?

En fait, j'ai trouvé pour f '(x)=-6+2400/x²

f'(x) = ( -6 x² +2400 ) / x²
= (-6( x² -400 )) / x²
= ( - 6 ( x + 20 ) ( x - 20 ) ) / x²

Après je suis bloquée..

Un produit de facteurs est nul si et seulement si .....

si l'un de ses facteurs est nul.
mais je ne comprends pas le calcul..

f'(x) = ( - 6 ( x + 20 ) ( x - 20 ) ) / x²

donc f'(x) = 0 si x+20 = 0 ou x - 20 = 0
soit x = ...

soit x = -20 ou x = 20
Apres j'ai fait un tableau de variation, est t-il bon? Je n'ai pas mis -20 dans le tableau parce que l'ensemble de définition était de ]0 ; + inf [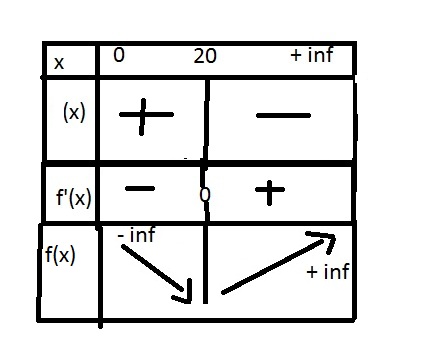

Tableau de variation

Bonsoir,

A quoi correspond la deuxième ligne du tableau ?
Comment trouves-tu le signe de la dérivée ?

La deuxième ligne correspond aux variations de f'(x).
J'ai trouvé les signes grace au signe de x et d'apres la calculatrice

Mais si x = 10, f'(x) = 18 > 0
donc pour x compris dans l'intervalle ]0 ; 20]
fonction croissante !!

Comment as tu trouvé x =10, f'(x) = 18 ?
Je ne vois pas

J'ai choisi une valeur de x au hasard qui permet de vérifier que ton tableau de variation est faux.
Tu peux prendre une autre valeur.

Ah d'accord.
Donc en fait, f'(x) est positif sur [0;20] et negatif ensuite?

C'est correct.

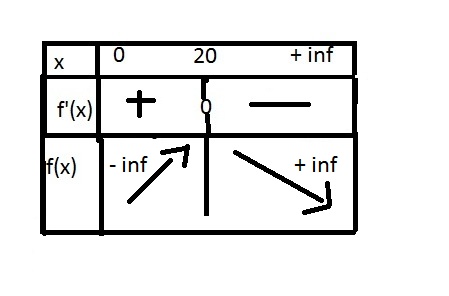
Le tableau est donc : ( voir image ) ? tableau de variation

Ensuite je dois préciser le maximum de la fonction f et la valeur de x correspondante. Je dois utiliser la calculatrice pour cela? ou c'est d'apres le tableau de variation? donc le maximum est de 20 ?

Oui,

Tu utilises les résultats indiqués dans le tableau de variation pour trouver le maximum qui est atteint pour x = 20 est vaut f(20)
Calcule f(20)

donc : f (x) = 624 - 6x - 2 400/x
f(20) = 624 - 6 * 20 - 2400 / 20 = 384 ?

Oui, 384.

Ensuite pour déduire les dimensions d'une page pour obtenir une surface imprimable maximale

( l'énoncé était : Dans l'impression d'un livre, on doit respecter sur chaque page des marges de 2 cm à gauche et à droite, de 3 cm en haut et en bas. On désigne par x la mesure en centimètres de la largeur d'une page entière et par y la mesure en centimètres de sa hauteur. )

on doit faire :
A=(y-6)*(x-4)
Ai=xy-4y-6x+24
=600-4y-6x+24
=624-6x-2400/x

non?

C'est juste.

Cool
et pour calculer le pourcentage que représente cette aire maximale par rapport à l'aire totale d'une page, on doit utiliser le résultat d'avant?

Pour le calcul de l'aire maximale, tu dois étudier les variations de la fonction aire.

comment calcule t-on les variations de la fonction aire?

Etudie la fonction f(x) = =624-6x-2400/x

J'ai déja étudier la variation de f(x) dans les questions précédentes

exact, j'étais à la question 2.

Pour la c) divise l'aire maximale par l'aire totale de la page et donne le résultat en pourcentage.

L'aire totale de la page est de 600cm² mais comment je peux trouver l'aire maximale?