theoreme de Fermat

[nishant]

bonjour tous j'ai un dm à faire sur la congruence . mais je n'arrive pas à faire.

1)demontrer que si p est premier alors(a+b)^p≡a^p+b^p mod(p)

j'ai reussi à demontrer . en utilisant la binome de newton

2. demontrer si p est premier (a+b+c)^p≡a^p+b^p+c^p mod (p)

je n'arrive pas faire cela
puis

3. montrer par recurrence si p est premier aors tout suite (a1+a2+....+an) d'entiers on a

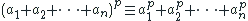mod(p)

je n'arrive pas faire le 2 et 3

[mathtous]

Bonjour,
Pour la question 2, écris
$(a+b+c{)}^p$ = $[(a+b)+c{]}^p$ et applique deux fois le résultat de la question 1.

[nishant]

ok merci

[mathtous]

De rien.