[Dm]Les fonctions cubiques et leur représentation

Bonjour,
Je me tourne une fois de plus vers vous et vos nobles conseils pour m'aider dans ce Dm, qui est à rendre pour le mardi de la semaine prochaine. Comme d'habitude, il consiste en deux parties ayant le même sujet (celui du titre).
Mon prof étant très rapidement passé aux exercices au lieu d'approfondir le cours et nous expliquer plus en détail ces nouvelles notions, je n'ai pas saisi grand-chose.
Alors, j'ai lu dans les fiches du forum le pdf de zauctore, mais je n'arrive pas à comprendre le dm...

Voici l'énoncé:

Citation
PARTIE 1
Soit la fonction f définie sur $mathbb{R}$ par f(x)=x³-3x+2. On appelle f' la fonction dérivée de f. Soit Cf la courbe représentative de f dans un repère ortho normé, avec 2 cm par unité. Une telle courbe définie par une fonction polynomiale de degré trois s'appelle une cubique.

Résoudre l'équation f(x)=0 en remarquant que deux des racines sont évidentes et simples.
2)Déterminer f'(x), puis résoudre f'(x)=0 et déterminer le signe de f'(x) selon les valeurs de x.
Faites le tablaeu de variation complet de la fonction f, en y faisant figurer les extrema locaux, les limites en l'infini, les intersections de Cf avec les axes.
Tracer avec soin Cf sur une feuille de papier millimétré.

Soit les trois points A (-2;0); B (0;2) et C (2;4). Les placer dans le repère.
5) Justifier brièvement l'alignement de ces points et prouver qu'ils sont tous les trois sur Cf.

La suite de l'exercice consiste à établir un résultat assez étonnant concernant les abscisses des points d'intersection entre une cubique et une droite sécante...
Soit deux points distincts M et N quelconques de Cf d'abscisse respective m et n, donc m≠n.
6) Déterminer les ordonnées de M et N, puis l'équation de la droite (MN) sous la forme y=ax+b.
7) Résoudre l'équation f(x)=ax+b, c'est-à-dire chercehr les intersections de Cf et de (MN)
Aide: les points M et N étant par construction sur Cf, l'équation du troisième degre admet nécessairement les solutions $x_1$ =m et $x_2$ =n, c'est donc seulement la troisième solution $x_3$ qu'on recherche et qui présente un intérêt. C'est l'abscisse d'un point P, la troisième intersection.
Calculez la somme des solutions $x$ _1 $+ x$ _2 $x_3$ , c'est-à-dire la somme des abscisses de M,N et P.

Pour le 1), j'ai trouvé f(x)=0 si x=1 ou si x=√1. Est-ce bon?
Et après, comment fait-on pour déterminer f'(x)?

Je vous remercie d'avance

PS: grâce à vous, j'ai réussi à avoir au précédant Dm 10/26 que le prof à mis sur 20, donc 10/20. Merci :D!

Bonsoir,

x = 1 n'est pas la seule racine, cherche l'autre racine évidente.

Pour la dérivée,
quelle est la dérivée de x³ ?
de -3x+2 ?

Merci de la réponse

Il y a aussi f(x)=0 si x=-2 ou si x=-√4.

Pour les dérivées (si j'ai bien compris):
de x³ -> 3.x²
de -3x+2 -> -1.

Donc, f'(x)= 3.x²-1 ... ?

La dérivée de -3x+2 est -3.

D'accord.
Donc f'(x)= 3.x²-3.

On factorise pour effectuer le tableau plus tard. Ce qui donne f'(x)= 3x(x-1). Voici mon tableau:

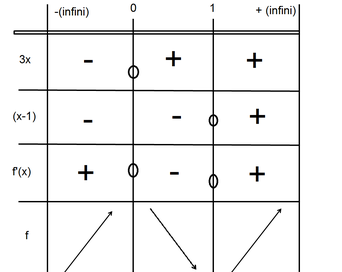
Tableau variation

Par contre, je n'arrive pas à trouver les points où se coupe la courbe dans la dernière partie du tableau (f)... Pourriez-vous m'aider?

La factorisation est fausse
3x² - 3 = 3(x²-1) = 3( .... ) ( ......)

Ah ok!
3x² - 3 = 3(x²-1) = 3(x)(x-1) ...?

Non

3x² - 3 = 3(x²-1) = 3(x+1)(x-1)

Alors, si je comprends bien, les termes du tableau seront 3(x+1) et (x-1)?

Oui,

Ou (x+1) et (x-1) car 3 >0

Okay!
Mais après, comment fait-on pour trouver les valeurs des flèches?

Construis le tableau de signes.

Le tableau est exactement le même, sauf que les valeurs de la première ligne sont: - [infini], -1, 1 et + [infini] et que les deux premières valeurs de la colonne de gauche sont (x+1) et (x-1).

(Désolé, j'ai changé d'ordinateur et je n'ai plus le tableau que j'avais fait )

Et pour le produit les signes sont ?

Alors, respectivement:
(x+1) -> -;+;+
(x-1) -> -;-;+
f'(x) -> +;-;+

C'est correct.

Super :D!
Et pour que le tableau soit complet, il ne faut pas mettre des valeurs sur les flèches?

Tu calcules les valeurs de la fonction f pour les valeurs de x correspondantes.

Euh... comment fait-on ?

Calcule
f(1)
soit 1³ - 3 + 2 = ...
puis
f(-1)

Puis les limites.

Ah d'accord!
Donc f(1)=1³-3+2=0
et f(-1)=-2.

Vérifie le calcul pour f(-1)

Ben f(-1)=-1³-3+2=-2

Non
f(-1) = (-1)³-3*(-1)+2
= ....

Ah oui mince, j'avais complètement zappé le x ^^...
Ce qui donne f(-1)=4

oui, f(-1) = 4.

Ok super! Merci beaucoup!