fonction résonner démontré

[taxeatomic]

Bonjours je ne comprend rien a cette exercice avec toutes les question

ABC est un triangle équilatéral de côte 12 cm et i est le milieu du segment [AB]
M est un point variable du segment [AI] et N est le point du segment [AB]distinct de M tel que AM=NB
Q est le point du segment [BC] et P est le point du segment [AC] tels que MNOPQ soit un rectangle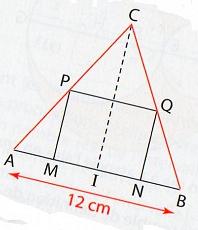

On note f la fonction qui à x=AM (en cm) associe l'aire,en cm², du rectangle MNOPQ

a)Quel est l'ensemble de définition de f?

b) Exprimer MN, puis MP en fonction de x

en déduire l'expression algébrique de f(x)

c) Calculer f(3), puis vérifier que pour tout x de [0;6[ : f(x)-f(3)=-2√3 (x-3)²

notez que "le (x-3)² n'est pas sous la racine" :rolling_eyes:

d) En déduire que f(3) est le maximum de f sur l'intervalle semi-ouvert[0;6[

e) Quelle sont les dimensions du rectangle d'aire maximal ?

merci d'avance

[Zauctore]

Bonjour

Rien compris, du tout ?

Prenons a) : x, c'est la longueur AM.
Observe la figure : AM est au moins égale à 0 et au plus à ... combien ?

Prenons b) : x, c'est la longueur AM.
Par symétrie, BN aussi est égal à x.
Alors que reste-t-il pour MN ? ça sera donné en fonction de x bien entendu.

Ensuite, AIC montre une configuration de Thalès version triangle... tu peux y appliquer ledit théorème pour trouver MP en fonction de x.

(peut-être qu'avant il faudra calculer IC, hauteur dans le triangle équilatérale de côté 12).