Déterminer le lieu géométrique de points dans l'espace
-
EElody* dernière édition par Hind
Bonjour,
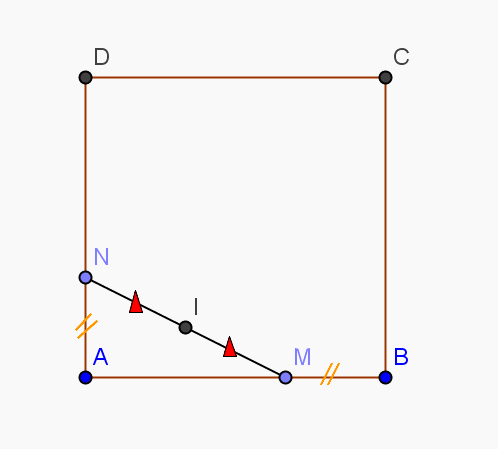
J'ai un DM de maths à faire et je suis bloquée. Pouvez vous m'aider s'il vous plaît ?ABCD est un carré. M est un point de [AB] et N un point de [AD] tel que AN = MB. On note enfin I le milieu de [NM].
On veut démontrer que le lieu de I lorsque M se déplace sur [AB] est un segment.
On se place dans le repère (A;vectAB;vectAC). On note t = AM.
-
A quel intervalle t appartient-il ?
--> à l'intervalle [0;1] (je ne sais pas si je dois justifier) -
Déterminer les coordonnées de I en fonction de t.
--> I est le milieu de [MN] donc I((xM+xN)/2;(yM+xN)/2)
M(t;0)
MB = AN
MB = 1-t
AN = 1-t donc N(0;1-t)
DONC I(t/2;(1-t)/2)
3)Montrer que les coordonnées (x;y) de I vérifient l'équation: y = 1/2-x pour tout x ∈ [0;1/2]
--> y = 1/2 - (1-t)/2
y = (1-t)/2
Les coordonnées de I vérifient l'équation y = 1/2-x-
Montrer que si un point J(x';y') a des coordonnées vérifiant l'équation: y' = 1/2-x' pour tout x' ∈ [0;1/2], alors il existe M', un point de [AB], et N' un point de [AD] tels que AN' = M'B et tels que J soit le milieu de [M'N'].
--> je n'arrive pas à répondre à cette question. -
Conclure
-
-
EElody* dernière édition par
J'ai oublié de préciser que la prof nous a dit qu'il fallait reprendre la question 3 pour répondre à la 4.
J'espère que quelqu'un pourra m'aider. Merci d'avance.