Fonction logarithme neperien

Bonjour, voila j'ai un probleme avec un sujet sur le ln

On admettra que les fonctions considérées dans cet exercice sont dérivables sur l’intervalle ]0; +∞[.
Soit la fonction f définie sur l’intervalle ]0; +∞[ par : f (x) = (2−lnx) lnx.
La figure ci-dessous donne la courbe représentative Cf de la fonction f dans un repère orthonormal ¡O;~ı,~ ¢ .

.

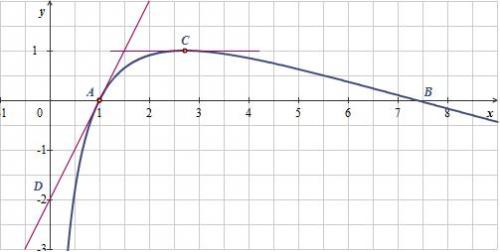
La courbe Cf coupe l’axe des abscisses en A(1; 0) et en B.
La tangente en C à la courbe Cf est parallèle à l’axe des abscisses et la tangente en A à la courbe Cf coupe l’axe des
ordonnées en D.

Déterminer l’abscisse du point B (la valeur exacte est demandée).
Calculer la limite de f en 0 et la limite de f en +∞.
On note f ′ la fonction dérivée de f sur ]0; +∞[.
(a) Démontrer que pour tout réel x de l’intervalle ]0; +∞[, f ′(x) =
2(1−lnx)
x .
(b) Déterminer les coordonnées du point C et l’ordonnée du point D (les valeurs exactes sont demandées).

Pour la premiere question je suppose qu'il faut trouver pour quand f(x) = 0, mais je n'arrive pas à resoudre l'equation :

lnx(2-lnx) = 0

Merci de votre aide

Bonjour,
lnx(2-lnx) = 0 c'est un produit nul.
Ou bien ln x = 0 ce qui redonne le point A,
Ou bien 2 - ln x = 0 ce qui donne x = ??

2-lnx = 0
lnx = 2 ?
x = 2/ln

Citation
x = 2/lnln n'est pas un nombre, c'est une fonction !
C'est comme si tu écrivais : √x = 2 donc x = 2/√ !!

Regarde l'autre solution : ln(x) = 0 donc x = 1 ( pour le point A ).

Ici, ln(x) = a , donc x = ? Il faut revoir ce que signifie la fonction ln, et son lien avec la fonction exponentielle.

ln(x)= a donc x= e^a

Oui, Ici, ln(x) = 2 donc x = e², valeur exacte.

Merci !
Pour lim f(x) en 0 je trouve -∞
Et pour limf(x) en +∞ je trouve +∞
Est ce correct?

Bonsoir,

la limite en +∞ est fausse.
Quelle est la limite de lnx quand x tend vers +∞ ?
de - lnx ?

lim lnx quand x tend vers +∞ = +∞
donc lim -lnx quand x tend vers +∞ = -∞ ?

Oui, c'est juste.

D'accord merci !
Pour la question 3 pour C, j'ai cherché f'(x) = 0 et j'ai trouvé x = e
Mais je n'arrive pas à trouver les coordonnées.

Calcule f(e).

f(e) = 1
C ( e ; 1 )?

f(e) = 1
C ( e ; 1 )?

C'est juste.

Et pour D, il faut calculer la tangente à A ? Et D aura pour coordonnées (0; y) ?

Oui, cherche l'équation de la tangente au point A.

Oui j'ai trouvé y = 2x-2 donc D(0:-2) !
Merci

C'est correct.