parallélépipède rectangle

[lizzie]

Bonsoir,

Je n'arrive pas à résoudre ce problème de math. Pouvez-vous m'aider?

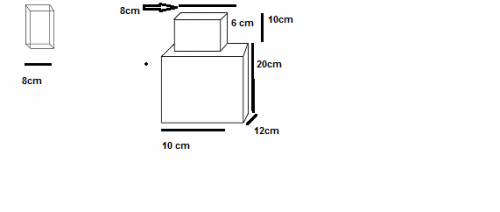
1) Calculer les volumes de ces deux réservoirs afin de montrer qu'ils ont le même volume. Rappel: la longueur L, la largeur l, et la hauteur h d'un parallélépipède rectangle sont les longueurs des arêtes issues d'un même sommet. Le volume d'un parallélépipède rectangle est: V=Llh

2) On remplit en même temps les deux réservoirs grâce à deux robinets qui fournissent la même quantité d'eau chaque seconde. Un des deux réservoirs sera-t-il rempli en premier?Pourquoi?

3) Dans quel réservoir l'eau montera le plus vite dans un premiertemps? A la fin? Pourquoi?

J'ai fait une erreur de reproduction. La figure 1 et la figure 2 ont la même taille mais pas la même largeur.

Merci de m'aider

[Noemi]

Bonsoir,

Indique tes éléments de calcul et la question qui te pose problème.
Calcule le volume.

[lizzie]

Noemi
Bonsoir,

Indique tes éléments de calcul et la question qui te pose problème.
Calcule le volume.
Bonsoir,
Pour le deuxième réservoir, je calcule :
V=101220=2400cm3 et V=8610=488cm3
V=2400+488=2888cm3
Par contre, je n'arrive pas à calculer le volume du 1er réservoir et je ne comprend pas le raisonnement de cet exo.

[Noemi]

Pour le volume du premier réservoir, quelles sont ses dimensions ?
largeur 8, hauteur 30 ? longueur 12 ?

Vu que le volume est le même, si les deux robinets ont le même débit alors .....

[lizzie]

Pour le premier réservoir, la prof nous a donné que la largeur= 8cm, le seul renseignement c'est qu'il a la même taille que le réservoir 2.
Désolé, je ne vois pas

[lizzie]

Pour le premier réservoir, la prof nous a donné que la largeur= 8cm, le seul renseignement c'est qu'il a la même taille que le réservoir 2.
Désolé, je ne vois pas

[Noemi]

Donc il faut supposer que la longueur vaut 12 cm.

[lizzie]

Nous sommes entrain d'étudier la proportionalité en classe??
Donc pour 1er réservoir:
V=812(10+20)=81230=2880cm3