Fonction volume d'un parallélépipède rectangle
-
NNew-ecliipse dernière édition par Hind
Bonjour, je bloque sur les questions suivantes, en rapport avec les deux images ci jointes :
- Justifier que, pour tout x de [0 ; 6 ], V(x)=x²(6-x)
- A) Démontrer que, pour tout x de [ 0 ; 6 ], V(x) - 16 = (2-x)(x-2-2-√3)(x-2+2√3)
B) Résoudre l'équation V(x) = 16. Quel(s) controle(s) peut on effectuer sur les solutions ?
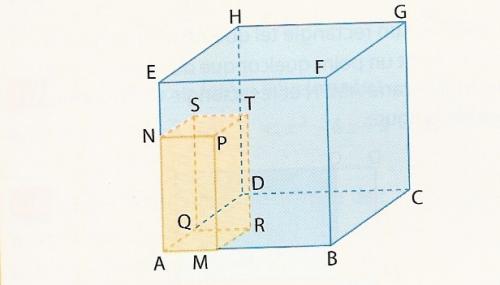
Cube : ABCDEFGH : cube de 6 cm de coté\r\nPour tout x de [ 0 ; 6 ] on place M sur [AB]et Q sur [AD] tels que AM = EN = AQ = x
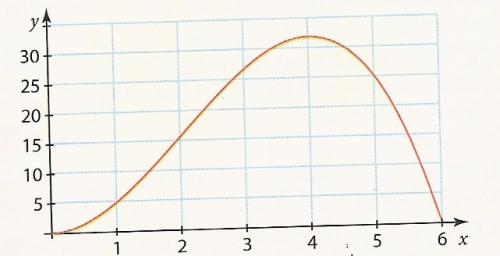
Graphique : Fonction V : Volume du Parallélépipède rectangle AMRQNPTS
edit : merci de donner des titres significatifs
-
Zauctore dernière édition par

Bonsoir New
Citation- Justifier que, pour tout x de [0 ; 6 ], V(x)=x²(6-x)
Le volume d'un pavé droit est le produit de ses dimensions l×L×h.
Bien entendu L et l sont égales à x, la base AMRQ étant un carré.
Maintenant, la hauteur AN est égale à AE-EN, soit...
Tu en déduiras le volume.
- Justifier que, pour tout x de [0 ; 6 ], V(x)=x²(6-x)
-
NNew-ecliipse dernière édition par
D'accord, mais pour formuler ma réponse, je dis juste que le volume d'un pavé droit est lxLxh, et que l & L sont égales à X, et queAn est égale à AE-EN soit 6-x ?
-
Zauctore dernière édition par

Oui et ainsi tu auras V = x×x×(6-x) = x²(6-x) comme attendu.
Citation
2. a) Démontrer que pour tout x de [0 ; 6] on a V(x) - 16 = (2-x)(x-2-2-√3)(x-2+2√3).
Tu t'y prendrais comment ?
-
NNew-ecliipse dernière édition par
Mais qu'est ce que le 16 sur la figure ?
-
Zauctore dernière édition par

On n'en a pas besoin pour cette question (tu verras son sens plus tard) : ici on ne fait que de l'algèbre. Il faut que tu montres que x²(6-x) -16 est égal à (2-x)(x-2-2-√3)(x-2+2√3), c'est tout (si l'on peut dire lol).
Comment vas-tu t'y prendre ?
-
Zauctore dernière édition par

Attention à la coquille : c'est (2-x)(x-2-2√3)(x-2+2√3) et pas (2-x)(x-2-2
-√3)(x-2+2√3).****
-
NNew-ecliipse dernière édition par
Il faut développer non ?
-
Zauctore dernière édition par

Voilà : développe chacune des expressions séparément puis regarde si les termes dans les deux développements sont les mêmes.
-
NNew-ecliipse dernière édition par
Donc : (2x-4-4√3)(2x-4+4√3) ? Et 6x²+x-16 ?
-
Zauctore dernière édition par

Pour développer (2-x)(x-2-2√3)(x-2+2√3), procède méthodiquement en commençant par (2-x)(x-2-2√3), et ensuite tu développeras le résultat sur (x-2+2√3).
C'est-à-dire que tu dois comprendre l'expression ainsi :
-
NNew-ecliipse dernière édition par
Donc cela donnerait : 2x-x²+x²-2x-2x√3 ?
-
Zauctore dernière édition par

J'ai :
(2-x)(x-2-2√3) = 2x - 4 - 4√3 - x² + 2x + 2x√3 = -x² + (4 + 2√3)x - 4 - 4√3.
-
NNew-ecliipse dernière édition par
Ah d'accord, je viens de comprendre ! & donc après il suffit de développer -x²+(4+2√3)x-4-4√3 avec (x-2+2√3) ?
-
Zauctore dernière édition par

oui
si tout est bon ça doit redonner 6x²+x-16 au final.
-
NNew-ecliipse dernière édition par
Mais hier je l'ai fais, & j'ai trouvé ceci, qui me semble tout de même bizarre : -x³+(4+2√3)x²-4x-4√3x + 2x²+4√3x+8-6√3 - 2√3x²+(4+2+2√3)x-2√3-2√3
-
Zauctore dernière édition par

Bonjour New
Alors si de cette façon tu es trop déroutée par les calculs et ça se conçoit, tu peux plutôt développer ce produit (2-x)(x-2-2√3)(x-2+2√3) en le regardant comme
(2-x)[
(x-2-2√3)(x-2+2√3)]
où tu peux t'aider d'une identité pour développer le produit rouge en 1er.Ensuite, j'ai laissé écrire une grosse ânerie : x²(6-x)-16 donne -x³+6x²-16 (au lieu de 6x²+x-16)

-
NNew-ecliipse dernière édition par
Le produit en rouge ferait donc : x²-2x+2x√3-2x+4+4√3-2x√3-4√3+√3 ?
-
NNew-ecliipse dernière édition par
Si on réduit ça fait donc : (2-x)x²-4x+4+√3 ?
-
Zauctore dernière édition par

non, le développement de (x-2-2√3)(x-2+2√3) ne montre plus de √3.
essaie encore.
-
NNew-ecliipse dernière édition par
Donc : x²-2x+2x√3-2x+4-4√3-2x√3+4√3
Réduction : x²-4x+4 ?
-
Zauctore dernière édition par

J'obtiens (x-2-2√3)(x-2+2√3) = x² - 4x - 8.
-
NNew-ecliipse dernière édition par
Pourquoi -8 ?
-
Zauctore dernière édition par

Développons :
(x-2-2√3)(x-2+2√3) = x² -2x + 2x√3 -2x + 4 -4√3 -2x√3 +4√3 -4√3²
Réduisons :
x² -2x + 2x√3 -2x + 4 -4√3 -2x√3 +4√3 -4√3² = x² -4x + 4 - 4×3 = x² -4x -8.
-
NNew-ecliipse dernière édition par
Ah d'accord !
Donc après : (2-x)x²-4x-8 = 2x²-8-16-x³+4x²+8x ?
-
Zauctore dernière édition par

Attention :
(2-x)(x²-4x-8) = 2x² -8
x-16 -x³ +4x² +8x = -x³ +6x² -16.
-
NNew-ecliipse dernière édition par
Ah oui effectivement. Faute d'inattention de ma part.
-
Zauctore dernière édition par

Maintenant, sachant que V(x) - 16 = (2-x)(x-2-2√3)(x-2+2√3)
Citation
B) Résoudre l'équation V(x) = 16.
Comment t'y prendrais-tu ?
-
NNew-ecliipse dernière édition par
V(x) = -x³+6x²-16
Donc : -x³+6x²-16 = 16
-x³+6x² = 16+16
-x³+6x² = 32 ?
& après je ne sais comment m'y prendre avec le ² et le ³
-
Zauctore dernière édition par

Ce qui est important, c'est sachant que V(x) - 16 = (2-x)(x-2-2√3)(x-2+2√3).
-
NNew-ecliipse dernière édition par
Donc : V(x)-16 = -x³ +6x² -16
Soit : = x²(6-x) - 16 = -x³ +6x² -16 ?
-
Zauctore dernière édition par

Bonjour New
Utilise la factorisation (2-x)(x-2-2√3)(x-2+2√3) !
Elle te donnera les valeurs qui rendent V(x) égal à 16.
-
NNew-ecliipse dernière édition par
Je ne comprends pas . .
-
Zauctore dernière édition par

V(x) = 16 équivaut à V(x) - 16 = 0
c'est-à-dire (2-x)(x-2-2√3)(x-2+2√3) = 0.
-
NNew-ecliipse dernière édition par
Je ne vois pas . .
-
Zauctore dernière édition par

allons New, un effort s'impose !
-
NNew-ecliipse dernière édition par
Zauctore
V(x) = 16 équivaut à V(x) - 16 = 0c'est-à-dire (2-x)(x-2-2√3)(x-2+2√3) = 0.
Cela j'ai bien compris, mais comment formuler pour résoudre l'équation ?
-
Zauctore dernière édition par

c'est un produit nul : (2-x)(x-2-2√3)(x-2+2√3) = 0 a lieu si et seulement si l'un des facteurs est nul.
-
NNew-ecliipse dernière édition par
Donc, il suffit juste de dire cela ?
-
Zauctore dernière édition par

et trouver les trois solutions bien entendu !