Calcul d'aires, fonctions trapèze et triangle rectangle
-
Aaidermoisvp dernière édition par Casebas
bonjour, désolé de vous déranger mais j'aimerai avoir de l'aide pour mon dm de maths je suis en panique j'ai du mal.
Voici mon énoncé :
ABCD est un trapèze rectangle tel que AB=6, CD=2 et AD=4.
Un point M décrit le segment [AD]. On construit le rectangle AMNP avec N appartenant à [BC] et P appartenant à [AB]. On pose x=AM.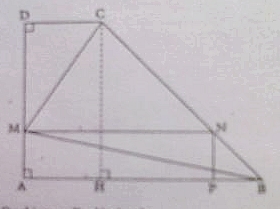
1. Quel intervalle décrit x?
Comme x=AM l'intervalle se situe entre AM mais je suis pas sur de ma réponse.2. Quelle est la nature du triangle BPN?
Ce triangle est rectangle d'après le dessin mais je n'arrive pas à expliquer pourquoi.3. En déduire BP en fonction de x.
Je pense que BP a la même mesure que AM donc c'est égale à x.4. Montrer que l'aire du rectangle AMNP est f(x)=-x²+6x
Aire du rectangle c'est L*l. L=AB-x et l=x donc cela ferait AB-x² et donc AB=6x mais je sais pas comment on peut le trouver celui-ci.5. Dresser le tableau de variation de la fonction f ainsi définie sur [0;4]
La fonction f est croissante puis décroissante, le sommet serait égale à -b/2a= -6/2*-1=-3 donc l'image de -3 = -9 mais après je sais pas comment faire avec l'intervalle de 0 et 4.6. Calculer l'aire de ABCD
Aire d'un trapèze = (B+b)*h/2
(AB+DC)AD/2= 82=167. En déduire que l'aire g(x) du triangle BMC est g(x)=12-2x
Aire d'un triangle B*h/2 mais je n'ai pas la hauteur je suis bloquer8. Tracer les courbes représentant les aires du rectangle AMNP et du triangle BMC
je ne suis pas sur à 100% du rectangle et le triangle je suis bloquer9. Déterminer les valeurs de x telles que:
a. l'aire du rectangle AMNP soit maximale
b.AMNP et BMC aient la même aire
c. l'aire de AMNP soit supérieure à celle de BMC
Je ne comprends pas du tout ce qu'il faut que je fasse ici.10. Expliquer comment vérifier graphiquement les résultats de la question 5.
J'espère que vous pourriez m'aider je vous remercie d'avance et si vous m'aidez sa sera grâce à vous que je comprendrais merci encore et à très vite j'espère!!!
-
Zauctore dernière édition par

Bonjour
Citation- Quel intervalle décrit x?
Comme x=AM l'intervalle se situe entre AM mais je suis pas sur de ma réponse.
x, c'est la longueur entre A et M ; tu vois bien que cette longueur est au minimum égale à 0 lorsque A et M sont confondus et au maximum ... l'info utile dans l'énoncé pour répondre à cette question est la phrase "anodine" Un point M décrit le segment [AD].
- Quel intervalle décrit x?
-
Aaidermoisvp dernière édition par
Zauctore
Bonjour
Citation- Quel intervalle décrit x?
Comme x=AM l'intervalle se situe entre AM mais je suis pas sur de ma réponse.
x, c'est la longueur entre A et M ; tu vois bien que cette longueur est au minimum égale à 0 lorsque A et M sont confondus et au maximum ... l'info utile dans l'énoncé pour répondre à cette question est la phrase "anodine" Un point M décrit le segment [AD].
a okok mais l'intervalle je vois pas ce que sa pourrai etre
- Quel intervalle décrit x?
-
Zauctore dernière édition par

au maximum, la longueur AM est égale à ?
-
Aaidermoisvp dernière édition par
0 non?
-
Zauctore dernière édition par

Bon alors imagine que le segment AD est une tige en bois sur laquelle bouge le point M (une bestiole qui se promène sur la tige). Avec ta règle tu mesures l'écart entre le point A et le point M. On pose toujours la graduation 0 sur le point A.
Au minimum, c'est ce que j'ai dit tout à l'heure, la longueur AM est égale à 0 : c'est quand la bestiole M est sur le point A.
Au maximum, c'est lorsque la bestiole est à l'autre bout de la tige : sur le point D. Alors dans ce cas, quelle longueur mesurerais-tu avec ta règle entre le point A et le point M (confondu avec D) ?
-
Aaidermoisvp dernière édition par
Zauctore
Bon alors imagine que le segment AD est une tige en bois sur laquelle bouge le point M (une bestiole qui se promène sur la tige). Avec ta règle tu mesures l'écart entre le point A et le point M. On pose toujours la graduation 0 sur le point A.Au minimum, c'est ce que j'ai dit tout à l'heure, la longueur AM est égale à 0 : c'est quand la bestiole M est sur le point A.
Au maximum, c'est lorsque la bestiole est à l'autre bout de la tige : sur le point D. Alors dans ce cas, quelle longueur mesurerais-tu avec ta règle entre le point A et le point M (confondu avec D) ?
je mesurerai la longueur AD-MD non?
désolé j'ai trop du mal
-
Zauctore dernière édition par

Non
C'est moi qui suis désolé

Voici qui t'aidera peut-être à comprendre ce qu'est la longueur AM lorsque M décrit [AD] :
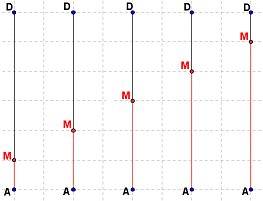
C'est la longueur de la ligne rouge, hein ! Donc au minimum sa longueur est 0 quand M est sur A (il n'y a pas de ligne rouge) et au maximum, c'est ...
-
Aaidermoisvp dernière édition par
Zauctore
NonC'est moi qui suis désolé

Voici qui t'aidera peut-être à comprendre ce qu'est la longueur AM lorsque M décrit [AD] :

C'est la longueur de la ligne rouge, hein ! Donc au minimum sa longueur est 0 quand M est sur A (il n'y a pas de ligne rouge) et au maximum, c'est ...C'est 6 si M se confond avec D ??
-
Zauctore dernière édition par

Voilà !
Donc au moins c'est 0 et au plus c'est 6 : la longueur x varie entre ces valeurs et ainsi x appartient à l'intervalle...
-
Aaidermoisvp dernière édition par
Zauctore
Voilà !Donc au moins c'est 0 et au plus c'est 4 (dans ton exo) : la longueur x varie entre ces valeurs et ainsi x appartient à l'intervalle...
[0;4]
-
Zauctore dernière édition par

oui.
-
Aaidermoisvp dernière édition par
Merci beaucoup est ce que tu pourrai m'aider pour les autres question stp si tu peux
-
Zauctore dernière édition par

Citation
2. Quelle est la nature du triangle BPN?
Ce triangle est rectangle d'après le dessin mais je n'arrive pas à expliquer pourquoi.
Ce triangle est un triangle rectangle en P car l'angle APN est droit : AMNP est un rectangle..Citation
3. En déduire BP en fonction de x.
Je pense que BP a la même mesure que AM donc c'est égale à x.
C'est NP qui est égal à x. Pense au théorème de Thalès pour trouver BP.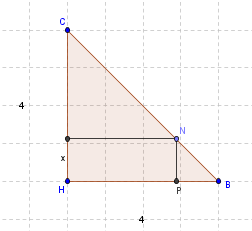
Ou bien réfléchis à la nature du triangle BHC.
-
Aaidermoisvp dernière édition par
est ce qu'on pourrait dire que BP est sur la droite HP et faire Thalès mais on a pas de mesure pour HB comment je pourrai faire svp?
-
Aaidermoisvp dernière édition par
aidermoisvp
est ce qu'on pourrait dire que BP est sur la droite HP et faire Thalès mais on a pas de mesure pour HB comment je pourrai faire svp?et je viens de remarquer que HBC est un triangle isocèle donc on pourrait dire que PBN y est aussi mais comment expliquer?
-
Zauctore dernière édition par

Par des considérations angulaires. Détermine la mesure de l'angle HBC.
-
Aaidermoisvp dernière édition par
langle HBC est de 45° vu que c'est un triangle isocèle mais je ne vois pas à quoi sa sert de chercher l'angle peux tu m'expliquer s'il te plait?
-
Zauctore dernière édition par

Et le 2e angle aigu du triangle BPN vaut combien ? je te rappelle que BPN est un triangle rectangle...
Bon je reviens plus tard dans la soirée.
-
Aaidermoisvp dernière édition par
Zauctore
Et le 2e angle aigu du triangle BPN vaut combien ? je te rappelle que BPN est un triangle rectangle...Bon je reviens plus tard dans la soirée.
-
Zauctore dernière édition par

Tu as réglé la question de la nature de BPN ?
Ce triangle est rectangle-isocèle en P.
-
Aaidermoisvp dernière édition par
Zauctore
Tu as réglé la question de la nature de BPN ?
Ce triangle est rectangle-isocèle en P.je vois qu'il est bien isocèle en P mais en fonction de x j'y arrive pas
-
Aaidermoisvp dernière édition par
PBN est un trianle isocèle et rectangle en P donc PB et NP sont donc égaux donc c'est égale à x nn?
-
Zauctore dernière édition par

Oui
J'espère que tu as compris pourquoi ce triangle est rectangle isocèle.
Maintenant pour demain il faut que tu réfléchisses mieux à
Citation
4. Montrer que l'aire du rectangle AMNP est f(x)=-x²+6xEn effet, ce que tu as raconté à propos de cette question (en dehors de la formule correcte) est assez fantaisiste.
Quelle est la longueur du rectangle AMNP ? Quelle est sa largeur (sur la figure initiale que tu as fournie) ?
Les deux dimensions sont fonction de x évidemment.A demain.
-
Aaidermoisvp dernière édition par
Merci beaucoup à demain...
-
Aaidermoisvp dernière édition par
Bonjour, alors j'ai réfléchie pour la question j'ai trouvé que la largeur du rectangle est x donc si on les multiplie sa fera -x².
Puis pour la longueur j'ai trouver 6x, le 6 correspond à la mesure de AB et x à PB.merci d'avance
-
Zauctore dernière édition par

Bonjour
C'est très artisanal...
Il faut que tu trouves une meilleure expression pour la longueur : AP est égal à AB-BP, soit en remplaçant...
-
Aaidermoisvp dernière édition par
Zauctore
BonjourC'est très artisanal...
Il faut que tu trouves une meilleure expression pour la longueur : AP est égal à AB-BP, soit en remplaçant...
Bonjour désolé de ne pas avoir répondu j'ai eu des soucis de santé.
on remplace BP par x et AB par 6 nn?
-
Zauctore dernière édition par

Ce sont les fêtes

Pour l'aire, on a donc AP×AM = (6-x)×x.
On retrouve bien -x²+6x lorsqu'on développe. Note bien qu'il ne fallait pas chercher à soustraire dans le calcul de l'aire.
-
Aaidermoisvp dernière édition par
Zauctore
Ce sont les fêtes
Pour l'aire, on a donc AP×AM = (6-x)×x.
On retrouve bien -x²+6x lorsqu'on développe. Note bien qu'il ne fallait pas chercher à soustraire dans le calcul de l'aire.
Merci beaucoup, c'est surement les fêtes comme tu dis...

Est ce que pour la question suivante tu pourrai m'expliquer car je trouve le sommet et l'image mais avec l'intervalle il n'y a pas de solution?
-
Aaidermoisvp dernière édition par
Pour le tableau de variation en faite je m'étais trompé mais je suis bloquer avec l'intervalle 0 et 4 je sais pas si il faut calculer f(0) et f(4) aussi pour indiquer que x appartient à tel intervalle ?
Voici le tableau que j'ai fait...
-
Aaidermoisvp dernière édition par
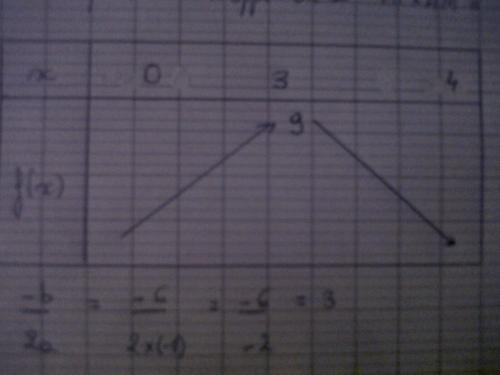
-
Zauctore dernière édition par

oui, il faut mettre les valeurs au bornes f(0) et f(4) dans ce genre de tableau. il faut donc les calculer.
-
Aaidermoisvp dernière édition par
Zauctore
oui, il faut mettre les valeurs au bornes f(0) et f(4) dans ce genre de tableau. il faut donc les calculer.okok et une fois calculer c'est que x est compris entre ces deux valeurs??
-
Aaidermoisvp dernière édition par
aidermoisvp
Zauctore
oui, il faut mettre les valeurs au bornes f(0) et f(4) dans ce genre de tableau. il faut donc les calculer.okok et une fois calculer c'est que x est compris entre ces deux valeurs??
Et l'aire de ABCD est-elle bien calculer?
merci beaucoup de m'aider
-
Zauctore dernière édition par

ABCD trapèze de bases AB=6 et CD=2, de hauteur AD = 4.
Son aire est donc (6+2)×4/2 = 16, ok.
-
Aaidermoisvp dernière édition par
Zauctore
ABCD trapèze de bases AB=6 et CD=2, de hauteur AD = 4.
Son aire est donc (6+2)×4/2 = 16, ok.Peux tu m'aider pour la question 7, car on a que une longueur et je vois pas du tout comment je pourrai faire
-
Zauctore dernière édition par

Regarde bien : il y a un lien avec la question précédente.
Tu seras d'accord avec moi que le triangle BMC est obtenu à partir du trapèze ABCD, oui certes ; mais de quelle façon ?
-
Aaidermoisvp dernière édition par
Zauctore
Regarde bien : il y a un lien avec la question précédente.Tu seras d'accord avec moi que le triangle BMC est obtenu à partir du trapèze ABCD, oui certes ; mais de quelle façon ?
Le triangle BMC est comment dire inscrit dans le trapèze ABCD (je sais pas si ça se dit inscrit)
-
Zauctore dernière édition par

Non, c'est plutôt du découpage : il faut enlever des morceaux à ABCD pour former BMC ; lesquels ?