Montrer que des droites sont concourants en utilisant le barycentre

BONJOUR ET BONNE ANNEE!

voici l'énoncé :

ABC est un triangle du plan, et A', B' et C' sont les milieux respectifs des segments [BC], [CA], et [AB].
On définit le point D par l'égalité vectorielle AD = 1/3 AB
Montrer que (AA'), (B'C') et (CD) sont concourantes.

Piste : utiliser le barycentre de (A,2) (B,1) (C,1)

Alors, j'ai fait le barycentre des points A, B et C
et j'ai trouvé AG = 1/4 AB + 1/4 AC

et je ne sais pas quoi faire maintenant ... faire le barycentre de A', B', C' ?

Une explication ne serait pas de tout refus.
Merci d'avance pour une réponse éclairée.
Cordialement, Elow'.
Sincères salutations à l'équipe.

Bonsoir

figure :

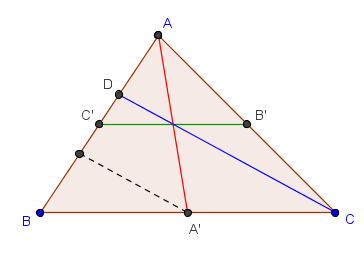
$fichier math$

est-on obligé d'utiliser des barycentres ? car avec les théorèmes des milieux on peut s'en sortir... cf page 4 de ce résumé pour des rappels de cours.

En fait, la piste me dit d'utiliser le barycentre de (A;2) (B;1) et (C;1)
donc je suppose qu'il faut faire avec les barycentres ...

Et sans eux, tu saurais faire ? Car ce n'est donc pas une obligation.

Oui je pense que je pourrais me débrouiller sans les barycentres.

mais montrez moi comment faire avec les barycentres s'il vous plait
j'ai un controle la semaine prochaine, mais je n'ai pas franchement compris cette leçon.

j'ai fait le barycentre des points A, B et C
et j'ai trouvé AG = 1/4 AB + 1/4 AC

ok, c'est bien dommage

AG = 1/4 AB + 1/4 AC définit le point G au milieu de la médiane AA' car c'est 1/4(AB + AC) = 1/4 (2AA') = 1/2 AA' - propriété géométrique élémentaire.

Or, par associativité, je vois que le barycentre de (A,2) (B,1) (C,1) peut être vu comme celui de (...,3) et (C,1).

Essaie de poursuivre.

je dois faire avec C'B' = 1/2 BC ?

non : le barycentre de (A,2) (B,1).

je dois montrer que G appartient à B'C' ?

j'ai trouvé AG = 1/3 AB
donc AG = AD

Si tu veux prouver cela, écris AG = 1/4 AB + 1/4 AC = 1/2(
1/2 AB + 1/2 AC).

et réfléchis à ce qui est en rouge.

donc AG = 1/2 AC' + 1/2 AB'
donc G est le barycentre de A, B', C' et se situe sur B'C' ?

Non : quel est le point qui est défini par 1/2 AC' + 1/2 AB' géométriquement ?

le point G ....?

oui, mais en dehors de ça ?

le centre de gravité ....?

Non : 1/2 (AC' + AB')

D'ailleurs je crois avoir déjà donné la réponse plus haut.

Enfin ça dépend de quel triangle tu parles.

Oui, mais que faire une fois que j'ai démontré que AG = 1/2 (AC' + AB' ) ..?

AC' + AB' = ... ?

AA'

ok