Polynôme de degrès 3

Bonjour à toutes et à tous .

J'ai un problème pour résoudre une équation cubique qui est : p(x)= ax³+bx²+cx+d
J'ai cherché les sujets qui traiter à peu près le même exercice que le mien , mais malheureusement je ne parviens toujours pas à comprendre.

1er Question : Trouver La valeur "d" en sachant que la courbe passe par A (0;2)
Ma réponse : f(0)=2 => d=2

2nd Question: Sachant que la courbe doit vérifier les conditions suivantes 1) et 2) et qu'elle passe par B, trouver les valeurs de a,b,c.

Il doit avoir une tangente en A parallèle au sol.
Il doit être tangente au sol au point B

C'est pour cette question que je demande de l'aide, je ne la comprends pas, enfin littéralement je l'ai compris, mais comment procéder pour trouver a,b,c ?

J'ai pensé à la méthode de "Factorisation d'un polynôme par Identification" mais cela me semble impossible (ou peut être que je me trompe).
Alors je me suis renseignée sur ce type de fonction et sur les différentes méthodes de résolution j'en ai trouvé deux: La méthode Cardan et et la méthode de Sotta , mais là encore il faudrait que je comprenne les formules ... Alors j'ai décidé de me tourner vers vous.

En ce qui concerne les conditions 1 et 2 j'ai pensé comme sa :
Nous sommes dans le cas d'un repère orthonormal ( O, i , j) O étant l'origine, O,j étant l'axe de verticale (ordonnée) et forcément O, i axe horizontale (Abscisse) nous savons que A (0;2), B(4;0)

Il doit avoir une tangente en A parallèle au sol.
Le sol à mon sens est l'axe des abscisse (O,i) donc la tangente serait une droite de coefficient directeur 0 passant par A.

2)Il doit être tangent au sol au point B.
Ici je suppose que cette tangente c'est l'axe des abscisses... (Mais là encore je ne suis pas sûr du tout de ce que je dis)

Voici une image pour comprendre un peu mieux ce que j'essaye de dire.
Mais il n'empêche que je n'avance pas dans cette exercice :rolling_eyes: quelqu'un aurait-il l'amabilité de me guider ?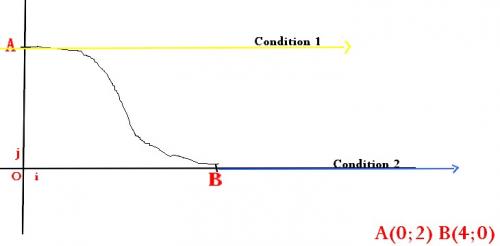

$fichier math$

Bonjour,
Tu dois savoir calculer le coefficient directeur d'une tangente à une courbe en un point de cette courbe en utilisant la dérivée.

Bonjour et merci d'essayer de m'aider.
Calculer le coefficient directeur d'une tangente ?
Je crois avoir mal compris mais il faudrait que je dérive P(x)?
ou je dois utiliser la formule f'(a) (x-a)+ f(a) ?

Il faut en effet dériver p(x).
Il suffit de connaître juste p'(x0) où x0 est l'abscisse du point considéré ( A ou B ).

Si je dérive p(x)= ax³+bx²+cx+d cela me donne alors
p'(x) =3ax²+2bx+c
A(0;2)
Ensuite p'(0)=3a0²+2b0+c ?

Oui, et que vaut p'(0) sachant que la tangente en A est horizontale ?

Elle vaut 0, non ?

Oui, ça te donne c=0.
Au tour de B maintenant :

la courbe passe par B
elle admet en B une tangente horizontale
Ces deux conditions te permettent de calculer a et b.

... p'(x) = 3ax²+2bx+0

La courbe passe par B de coordonnée (4;0) et en B il y a une tangente horizontale (donc de coefficient directeur 0)... la courbe et la tangente on un point commun B...
...Il y a t-il moyen d'expliquer plus clairement ? parce que j'avoue que la je vois pas trop comment obtenir a et b , et j'ai bien l'impression que ca doit être quelque chose de tout simple mais que j'ai tendance à compliquer.

Est ce qu'à partir du point B je dois encore remplacer x ?

Tu l'as fait pour A:
Tu as écrit :

la courbe passe par A d'abscisse 0 et d'ordonnée 2, donc p(0) = 2 : ça te donne d
la courbe admet en A une tangente horizontale, donc p'(0) = 0 : ça te donne c

Pour B, tu fais la même chose :

la courbe passe par B(4,0) donc p(4) = 0
la courbe admet en B une tangente horizontale donc p'(4) = 0
Ca te donne deux équations en a et b : un système que tu dois savoir résoudre.