Montrer que des droites sont concourantes

Bonjour,

Je suis élève de 1ère S avec des petites difficultés en maths. Je sais, vous allez me dire, que fous-tu en S? C'est une longue histoire... Passons aux choses sérieuses.
Ma prof de maths vient de me rendre un DM sur les barycentres. J'ai eu une très mauvaise note et le fait qu'elle n'ait pas fait de correction ne m'a pas du tout aidé!
Voici l'énoncé:

"Chacun des côtés d'un triangle ABC est partagé en 3 segments de mêmes longueurs grâce aux points: I et J sur [AB], K et L sur [BC], M et N sur [AC].

Démontrer que les droites (IL), (JM) et (KN) sont concourantes."

J'ai pensé aux barycentres partiels, mais je ne sais pas par où commencer!

Pourriez-vous me donner quelques astuces pour résoudre cette exercice?

Merci beaucoup ^^

Milly

Bonjour

Une figure pour lancer la discussion :

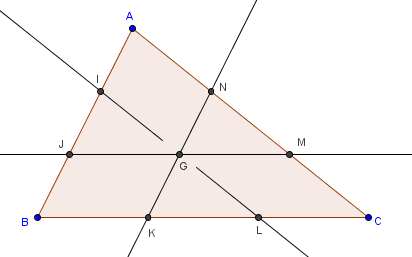
$fichier math$
J'appelle G le point de rencontre de (JM) et (KN) par exemple.
Il s'agit de prouver que (IL) passe par G.

Voyons, voyons : tu parles de barycentres partiels, peux-tu détailler un peu ?

Bonjour,

Merci d'avoir répondu. Mais il y a quelque chose que je ne comprends pas: comment prouvez-vous que G est le point de rencontre des droites (JN) et (KL) ?

Pour les barycentres partiels: on nomme G barycentre des points pondérés (A;1), (B;1) et (C;1). Après on sait que N∈[AC] donc on en déduit que G barycentre partiel des points pondérés (A;1) et (N;2). En gros, je pensais partir de là et trouver les autres. Et prouver ainsi que les 3 droites se coupaient en un seul point, le point G.
Je ne sais pas si mon raisonnement est bon, en revanche.

Encore merci ^^
Milly

Le fait que (JM) et (NK) soient sécantes n'a pas besoin d'être prouvé !

Je regarde tout-à-l'heure ton raisonnement.

Bonjour,

Merci pour votre aide. J'ai mieux compris et je vais essayer de suivre votre raisonnement.

Milly ^^

ABCD est un parallélogramme , H et K et L tel que
DK→ =(α+2) DB→
Et CL→= α BC→
Et α est un réel connu
Et M est l’intersection de (DL) et (CK)
Montrez que DM→ = (α+2)/( α²+2 α+2) DL→
La solution que je propose est :
Soit M’ un point tel que : D M’→ = (α+2)/( α²+2 α+2) DL→
Donc D M’→ - (α+2)/( α²+2 α+2) DL→ = 0
Ce qui veut dire ( α²+2 α+2) / ( α²+2 α+2) D M’→ - (α+2) /( α²+2 α+2) DL→ =0
( α²+2 α+2) D M’→ - (α+2) DL→ =0
(α²+2 α+2- α-2)M’D→ = -(α+2)M’L→
(α²+α) M’D→+(α+2) M’L→ =0
Donc M’ est barycentre de {(D,α²+α ), (L, α+2)}
M’ Є (DL)
D’autre part, on a
DK→ =(α+2) DB→
DK→ - (α+2) DB→ =0
-α DK→+ α(α+2) DB→=0
Donc en utilisant l’associativité (D,α²+α) est barycentre de {(K,-α), (B,α²+2α)}
Et aussi : CL→= α BC→

(1+α)LC→ = α LB→ donc (α+2)(α+1) LC→ - α(α+2)LB→ = 0
Ce qui veut dire que (L,α+2) est barycentre de {(C, (α+2)(α+1)) , (B, -α ( α+2))}
On a M’ est barycentre de {(D,α²+α ), (L, α+2)} donc M’ est barycentre de {(C, (α+2)(α+1)) , (B, -α ( α+2)), (K,-α), (B,α²+2α)}
M’ est barycentre de {(C, (α+2)(α+1)) , (B, -α ( α+2)), (K,-α), (B,α(α+2)) }
M’ est bary{(C, (α+2)(α+1)) , (K,-α)}
M’ appartient à (CK)
On a M’ Є (DL) et M’ Є (CK) donc M’ est l’intersection de (DL) et (CK) donc M’ = M
Conclusion : DM→ = (α+2)/( α²+2 α+2) DL→
les petites flêches au dessous des DL et DM et CL veulent dirent les vacteurs DM et CL et DM et non pas une distance