Système d'équation inéquations
-
Ggaelle94 dernière édition par
bonjour, j'ai un problème à résoudre et je ne sais pas du tout comment faire.
voila l'énnoncé :pour son anniversaire, Laura sait qu'elle va recevoir x€ de sa grand mère et y€ de sa grande soeur. Laura sait aussi que sa grand mère lui offre 150€ de plus que sa grande soeur et que sa grande soeur ne peut donner, au maximum, que la moitié de la somme de la grand mère.
Optimiste, laura pense que sa grand mère lui donnera au moins 20€.Déterminer géométriquement les couples(x;y) possibles.
pouvez-vous m'aider svp ??
-
Bonjour,
En quelle classe es-tu ?Quelles équations/inéquations as-tu pu écrire sur x et y ?
-
Ggaelle94 dernière édition par
en première ES.
y= x-150
y=x/2
x=y+150
-
Bonjour,
La relation y = x - 150 est juste.
il faut prendre en compte l'indication "au maximum", donc y ≤ x/2
puis l'indication "au moins 20 €"Fais la représentation graphique.
-
Ggaelle94 dernière édition par
y= x - 150
y ≤ x/2je me suis trompée c est au moins 200 €
et sur le graphique je mets les 2 fonctions que j'ai écrit au dessus c est ca ?
-
Donc x ≥ 200
Cherche le domaine solution en traçant les trois droites.
-
Ggaelle94 dernière édition par
la solution c'est quand les deux courbes se croises ?
-
Le point d'intersection donne un couple solution, il est demandé tous les couples possibles, donc tous les couples appartenant au domaine solution.
-
Ggaelle94 dernière édition par
et c'est quoi le domaine solution , je comprends pas :s
-
Tu cherches l'ensemble des points solution du système:
y= x - 150
y ≤ x/2
x ≥ 200
-
Ggaelle94 dernière édition par
d'accord merci
-
Ggaelle94 dernière édition par
ce sont les points qui sont à la fois sur la droite d'equation y=x-150 et les points qui sont en dessous de y≤/2 c'est ca ?
-
Tu prends tous les points qui vérifient :
y= x - 150
y ≤ x/2
x ≥ 200soit tous les points qui sont sur la droite d'équation y = x-150 pour
x≥ 200
et le x correspondant à l'abscisse du point d'intersection.
-
Ggaelle94 dernière édition par
oui mais pour y ≤ x/2 ?
-
Cette inéquation doit aussi être satisfaite.
-
Ggaelle94 dernière édition par
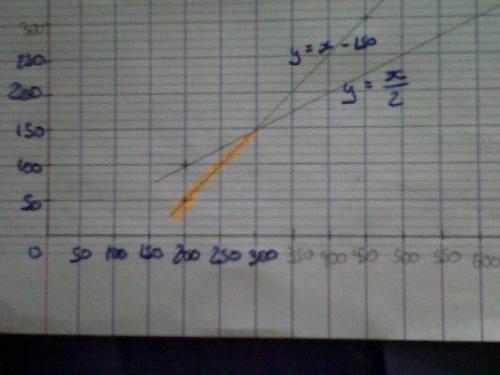
c'est ça la réponse ? ( en orange )
-
Oui a condition de débuter à x = 200.
-
Ggaelle94 dernière édition par
oui d'accord merci