[Fonction] équations, coordonnées...
-
MMarine64 dernière édition par
Voici l'énoncé:
f(x)= 2(x+3)(x-1)
c) Prouver que pour tout réel x, f(x) > ou = à -8
Résolver l'équation f(x)=-8
Trouver les coordonnées du point A.- La droite d'équation y=2 coupe P en I et J, calculer les coordonnées de ces points!
Graphique:
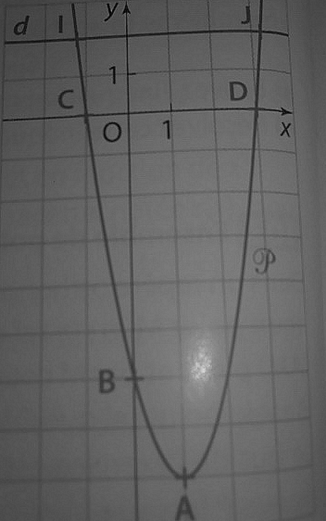
-
Ssamsoo dernière édition par
tu peux déjà commencer par développer pour essayer de résoudre f(x)=-8
-
MMarine64 dernière édition par
ben j'ai essayé:
f(x)=-8 donc
2(x+3)(x-1)=-8
<=> 2(x+3)(x-1)+8=0
<=> 2x²-4x-6+8=0
<=> 2x²-4x+2=0et la je suis pas sure de comment faire, parce qu'avec le x² c'est pas franchement pratique!
-
Ssamsoo dernière édition par
tu peux simplifier par 2 et ensuite tu factorise...
-
MMarine64 dernière édition par
j'ai essayé sa me donne un truc archi' faux..
tu veux bien me montrer please?
-
Ssamsoo dernière édition par
2x²-4x+2=0
<=> 2(x²-2x+1)=0
<=> x²-2x+1=0la on a une belle identité remarquable pour factoriser ^^
-
MMarine64 dernière édition par
donc oui identité remarque:
donc sa fait (x-1)²=0
<=> x-1=0 <=> x=1
c'est ce que j'avais fait, mais je sais pas pourquoi j'ai douté, j'y suis depuis tellement longtemps que je commence à stresser...etc
merci donc d'avoir confirmé ( en fait je me suis rendu compte que j'avais mis (x-1) <=> (1-1) donc 0 au lieu de x+1
-
MMarine64 dernière édition par
Maintenant je fais comment pour prouver, démontrer et bien rédiger le reste?
-
Ssamsoo dernière édition par
je viens de voir une erreur
f(x)=-8 donc
2(x+3)(x-1)=-8
<=> 2(x+3)(x-1)+8=0
<=> 2x²-4x-6+8=0 c'est 2x²+4x-6+8
<=> 2x²-4x+2=0 du cou c'est 2(x+1)²Soit f(x)=ax+b+c avec a≠0
si a>0 f décroissant sur ]-∞;-b/(2a)] et croissant sur [-b/(2a);+∞[
si a<0 f croissant sur ]-∞;-b/(2a)] et décroissant sur [-b/(2a);+∞[ca devrait aider pour répondre à: Prouver que pour tout réel x, f(x) ≥-8
-
MMarine64 dernière édition par
Non non c'est bien 2(x**-**1)²
si je développe sa donne bien sa:2(x²**-**2x+1)
<=> 2x²-4x
+2>> Il y a bien le +2
Sa ne change rien au produit nul (2*0=0)okey merci pou le reste!