Vecteurs (?) : carré, milieux, triangle rectangle isocèle...
-
Ssoso123 dernière édition par
Soit MNPQ un carré de centre O.
I et J sont les milieux respectifs de [MN] et [OP].
Démontrer que le triangle IJQ est isocèle et rectangle.
-
Zauctore dernière édition par

BONSOIR
non pardon j'ai répondu trop vite
deux sec je réfléchis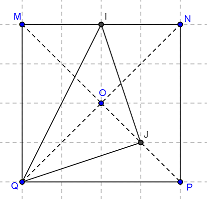
-
Ssoso123 dernière édition par
D'accord, merci beaucoup !
-
Zauctore dernière édition par

Une possibilité serait déjà de montrer l'égalité des côtés IJ et JQ via Pythagore:
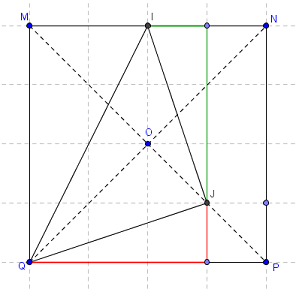
Observe les décompositions en couleur et raisonne à partir du côté a du carré (calcul littéral).Pour montrer que le triangle est de plus rectangle, je propose la réciproque de Pythagore, en calculant au préalable IQ² comme précédemment.
C'est très calculatoire, ce que je te propose là ! On verra comment tu t'en sors...
(Mille excuses pour ma réponse précipitée ci-avant.)
-
Ssoso123 dernière édition par
Merci beaucoup, je vais y réflechir demain matin.
-
Ssoso123 dernière édition par
On ne connait aucune longueur , comment faire ?
-
Zauctore dernière édition par

Raisonne à partir du côté a du carré (calcul littéral).
-
Ssoso123 dernière édition par
Et quel est le coté a ?
-
Zauctore dernière édition par

a est une longueur fixée quelconque ; calcula en fonction de a
sinon, mieux valant faire quelque chose plutôt que rien, commence par mener les calculs en prenant une valeur particulière, par exemple 10 cm et vois ce que cela donne.
-
Ssoso123 dernière édition par
Je comprend rien. Je croit que je vais pas y arriver :frowning2:
-
Ssoso123 dernière édition par
Il ne faudrait pas mettre la figure dans un repère (O,i→^\rightarrow→,j→^\rightarrow→)
Et prendre par exemple 1 cm pour les côtés du carré, puis calculer les coordonnés ?
-
Zauctore dernière édition par

Bonjour
Ce serait compliquer une chose simple.
Les côtés verts et rouges mesurent 3/4 a et a/4. Tu peux alors calculer les hypoténuses de chaque triangle avec Pythagore.