systeme linéaire
-
Ccharlotte dernière édition par
Bonjour,
Cel fais plusieurs heure que je suis sur mon devoir maison dont je n'arrive pas a faire la derniere question
En voici l'énoncé:Une P.M.E équipé d'un atelier d'électrnique et d'un atelier de montage fabrique deux types d'appareil :
- L'appareil A nécéssite 2 heures de travail dans l'atelier d'électronique et 45 minute (= 0,75 heure) dans l'atelier de montage. 2 puces entrent dans la fabrication de cet appareil.
- L'appareil B nécessite 1 heure et demi ( = 1,5 heure) de travail dans l'atelier d'éléctronique et 1 heure dans l'atelier de montage. 1 puce entre dans la fabrication de l'appareil B.
L'usine reçoit journellement 64 puces. L'atelier d'électronique compte 9 ouvriers et celui de mécanique en compte 5.
Chaque ouvier travaille 8 heures par jours.
L'entreprise réalise un bénéfice de 5 euros par appareil A vendu t de 3 euros par appareil B vendu.
On suppose que toute la production est vendue.
On appelle x le nombre d'appareils A fabriqués et y le nombre d'appareils B fabriqués.
Le but de l'exercice est de déterminer les entiers x et y permettant de réaliser chaque jour un bénéfice maximal;
-
montrer que les contraintes de cette situation peuvent être traduite par le systeme d'inéquations: (S)
x ≥ 0
y ≥ 0
y≤ -2x + 64
y + (4/3)x ≤ 48
y ≤ -(3/4)x +40 -
Dans le plan rapporté à un repere orthonormé (unité graphique: 1cm représente 5 unités), mettre en évidnce l'ensemble des points M(x;y) traduisant le systeme (S). Expliquer.
3)On note b le bénéfice réalisé par la fabrication de x appareils A et de y appareils B fabriqués.
Exprimer b en fonction de x et y.
Tracer la droite D correspondant à un bénéfice de 45€.- a) determiner gaphiquement le point I (x;y) pour lequel b est maximal, en expliquanr la méthode.
b) en deduire la valeur du bénéfice maximal.
J'ai deja fais toute les questions, sauf la 4) que je n'ai pas réussit a faire !!
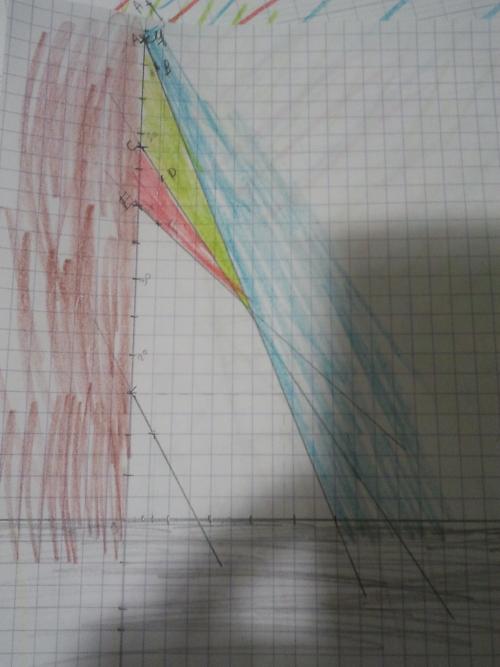
pour 2x + y ≤ 64 j'ai trouver que y = 64 - 2X j'ai fais ma droit grace au points A(0;64) et B(0;60)
pour (4/3)x +y≤48 et ai fais ma courbe grace aux point C ( 0;48) et D (3;44)
Pour -(3/4)x -y ≥-40 : E(0;40) et F(3;37,75).j'ai aussi tracer ma courbe pour un bénéfice de 45€.
Je vais essayer de mettre une photo de mon repère othonormé.
Je n'arrive pas a faire la question 4, sa fais déja plusieurs heures que j'i suis et je ne sais pas où placer mn point I !!
Merci d'avance
Charlotte
-
Ccharlotte dernière édition par
-
Bonjour,
Pour obtenir le bénéfice maximal, trace une parallèle à la droite bénéfice D qui coupe le domaine des possibles le plus éloignés possible du point O.
-
Ccharlotte dernière édition par
dans se cas mon point I est a la limite des parties coloriées et la droite va aller dans les parties coloriées ?
-
Juste à la limite.
-
Ccharlotte dernière édition par
merci beaucoup !!
