Calcul sur une suite (spirale fibonacci)

[low93]

Bonjour tout le monde.
Voici un exercice de mon dm sur les suites que je trouve particulièrement difficile! Je ne comprends pas et ne sais donc pas comment commencer...
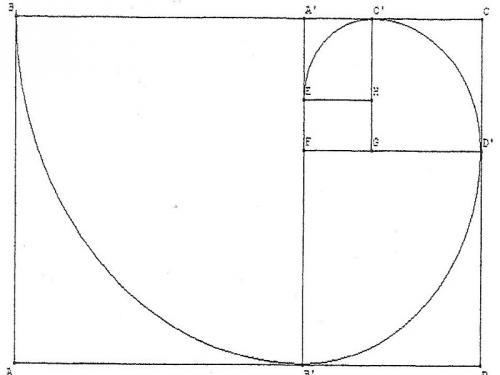
Merci d'avance de votre aide précieuse! :frowning2:

ABCD est un rectangle avec AB = 1 et CD = (>1). On construit le carré ABA'D', on obtient un nouveau rectangle A'CDB'. On réitère le procédé dans ce nouveau rectangle.

1. On souhaite que les rectangles gardent les mêmes proportions, autrement dit que le rapport Longueur/largeur soit constant. Déterminer la valeur de φ.

2. On appelle an la longueur du petit coté et bn la longueur du grand coté du n-ème rectangle. Donner la valeur de $a_n$ et de $b_$ pour n = 1; 2; 3

3. Exprimer $b_{n+1}$ et $a_{n+1}$ en fonction de $a_n$ et de $b_n$. En déduire l'expression de $a_{n+1}$en fonction de an;$a_{n-1}$

4. Démontrer que $a_2$ = (1/φ$)a_1$ et $a_3$= (1/φ$)a_2$.

5)Par un raisonnement de proche en proche démontrer que $a_{n+1}$ = $(1/phi)a_n$.

6. On réalise une spirale en joignant les quarts de cercle inscrits dans chaque carré. On appelle cn la longueur du quart de cercle du n-ème carré. Quel est la valeur de $c_n$ en fonction de φ?

7. Exprimer la longueur de la spirale au n-ème carré en fonction de φ.

[low93]

[mtschoon]

φBonjour,

Il s'agit de la construction des rectangles d'or ( tu peux trouver des informations sur le web)

Evidemment , la figure que tu joins est un peu déformée car les "carrés" sont des "rectangles"...je te suggère de faire une figure exacte ( pour mieux comprendre )

Piste pour démarrer :

Au rectangle ABCD on enève le carré BA'B'A
Le rectangle A'CDB' a les mêmes proportions que le rectangle ABCD

$\text{\varphi=\frac{bc}{ab}=\frac{cd}{a'c}$

AB=1 donc BC=φ , CD=φ , A'C=BC-BA'=BC-AB=φ-1

Donc :

$\text{\frac{\varphi}{1}=\frac{1}{\varphi-1}$

Tu fais les produits en croix , tu transposes , tu obtiens une équation du second degré qui tu résous.

Tu obtiens 2 solutions et tu conserves la solution supérieure à 1 ( vu que BC > AB)

( Tu dois trouver $\text{\varphi=\frac{1+\sqrt 5}{2}$ )