démonstration triangle rectangle

Bonjour,
Voilà j'ai fait mon deuxième exercice et je voudrais que l'on me dise s'il est juste. Merci pour toutes vos réponses!
Enoncé:
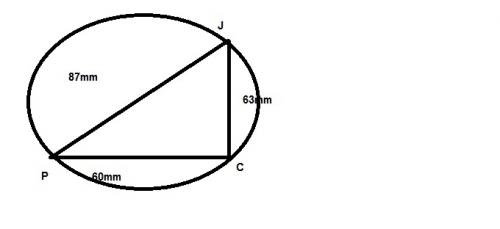
JCP est un triangle tel que CJ=63mm, CP=60mm et JP=87mm.

Montrer que le triangle JCP est rectangle et préciser en quel point.
Calculer le rayon du cercle circonscrit au triangle JCP. Justifier.
A) Quelle formule donne le périmètre d'un cercle ?
B) Calculer l'arrondi au mm du périmètre du cercle circonscrit au triangle JCP.
1)Selon pythagore:
JP²=CP²+CJ²
87²=60²+63²
7569=3600+3969
donc JCP est un triangle rectangle en C
Le cercle circonscrit au triangle admet pour diamètre l'hypoténuse du triangle rectangle donc le centre du cercle circonscrit se trouve au milieu de l'hypoténuse . So rayon vaut:
r=Hypoténuse /2= JP/2=87/2=43,5mm
A)Périmètre du cercle: 2×3,14×r
B) P=2×3,14×r
= 2×3,14×43,5=273,5mm
Est- ce juste?

Bonsoir,

Pour la question 1) c'est la réciproque du théorème de Pythagore qui est à utiliser.

Le reste est juste.