Démontrer l'alignement de points - Transformation, rotation et homothétie

bonjour a tous, j'aurais besoin d'aide pour un exercice de maths que je n'arrive pas à faire, voici l'ennoncé:

ABCZ, A'B'C'Z et A"B"C"Z sont trois carrés de sens direct. Les points A, A' et A" sont alignés sur une
Démontrer l'alignement des points C, C' et C".(On pourra utiliser une rotation)
Démontrer l'alignement des points B, B' et B". (On pourra utiliser une homothétie et une rotation)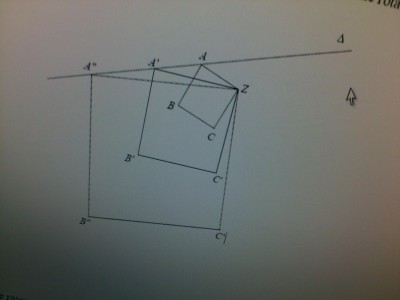

$fichier math$

Merci

Bonjour,

Piste pour la première question ,

je te suggère d'utiliser la rotation r de centre Z et d'angle Π/2

r(A)=... , r(A')=... , r(A")=...., donc........

Piste pour la seconde question ,

Tu prouves que :
$\text{zb=\sqrt 2 za et \ (\vec{za},\vec{zb})=\frac{\pi}{4} (2\pi)$
............
............

je te suggère d'utiliser la rotation de centre Z et d'angle Π/4 suivie de l'homothétie de centre Z et de rapport √2

bonjour voici ma réponse
la rotation r de centre Z et d'angle , alors dans chaque carré, on aura r(A)=C, r(A')=B' et r(A")=B''

comme une rotation conserve l'alignement c'est-à-dire qu'elle transforme trois points alignés AA'A''en trois points alignés CC'C''

est ca?merci

Oui !

Rebonjour pur la question j'ai démontrer comment on trouver racine de 2
pour la rotation je fais sachant que j'utilise la rotation de centre Z et d'angle Π/4
r(A)=B
r(A')=B'
r(A'') =B''
Est ca?parce que là je suis pas sur.
par contre je vois pas trop ce qu'il faut faire avec l'homothétie.
Merci pour l'aide

Non , car ZB ≠ ZA

Soit r rotation de centre Z et d'angle Π/4

Tu places $B_1$ tel que $r(A)=B_1$

Soit h l'homothétie de centre Z et de rapport √2 :

Tu auras alors $h(B_1$ )=B

Mêm principe pour A' et A"