Calculer le module et argument d'un nombre complexe

Bonjour;

Je dois calculer le module et l'argument de ce nombre complexe:

((1+i√3)/(1-i))^188

J'ai d'abord calculé le module sans la puissance 188 mais.. je tombe sur du √2 donc impossible de définir un argument puisque c'est supérieur à 1.

En gardant la puissance et calculant le quotient j'ai bien peur d'y rester dessus pendant 10/15 h .. alors je me demande s'il n'y a pas une formule pour calculer le quotient facilement avec une telle puissance...

Merci de votre aide.

Bonjour,

Mets le module en facteur.

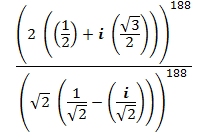$fichier math$ ... et aprés ?

Donc le module est ......

Calcule l'argument du numérateur et du dénominateur.

je trouve argument numérateur: 2(π/3) (module = 1)
dénominateur: (√2)(π/4) (module = 1)

Donc argument quotient sans la puissance 188): (√2)(π/12)

Non

Numérateur module 2 et argument π/3

Vérifie pour le dénominateur

Le deuxième est faux.

Tu as une relation arg(z1/z2) = arg(z1) ......

Oui,

Donc l'expression sans puissance a pour module .....
et pour argument .....

Puis tu calcules avec la puissance 188.

Sans puissance le quotient a pour module 2/√2 = √2 et pour argument 7π/12

Donc avec la puissance 188 : le quotient a pour module (√2)^188 et pour argument 329π/3 ?

Simplifie le module et l'argument.

329π/3 fraction irréductible ...

(√2)^188 = 2^94

329π/3 = k*2π + ......

329π/3 = 164π/3 + 2kπ

Non,

Cherche la valeur de k.

329π/3=π/3 + 2kπ ⇔ k=164/3

329π/3 = π/3 + 2(164/3)π c'est compliquer la tache ..

Non

k2π correspond au nombre de tours

exemple :
25π/4 = 24π/4 + π/4 = 6π + π/4 = 3*2π + π/4

329π/3 = 54*2π + 5π/3

oui,

donc l'argument est 5π/3.

Merci beaucoup :))

Sinon , une 2eme question:

Résoudre dans C :

2z²-(1+5i)z-2(1-i)=0

Δ = -8-6i

z1= ((1+5i)-i√(-8-6i))/4
z2= ((1+5i)+i√(-8-6i))/4

Je ne pense pas avoir bon car il me faut normalement trouver y²=Δ et avoir les solution z1 et z2 grâce à y ...

Pour un nouveau sujet, propose un autre post.

Le début est juste.
détermine un nombre complexe tel que z² = -8 - 6i