DM : Deux mouches se déplacent sur les faces d'une boite...
-
LLiliZazaMiss dernière édition par
Bonjour !
J'ai un petit problème dans mon Devoir de Math que je n'arrive pas a résoudre !
Pourriez vous m'aider s'il vous plait ?Deux mouches se déplacent sur les faces d'une boite a chaussure représentée par le pavé de la figure suivante. ABCDEFGH est un pavé droit de longueur AB= 8 cm, de largueur BC= 6cm et de hauteur BF= 4cm.
Elles se trouvent toutes les deux au point A et veulent se diriger au point G où se trouve de la nourriture.
La mouche 1 suit le trajet A,I,G où I est le milieu de [EF].
La mouche 2 suit le trajet A,J,G où J est le milieu de [BF].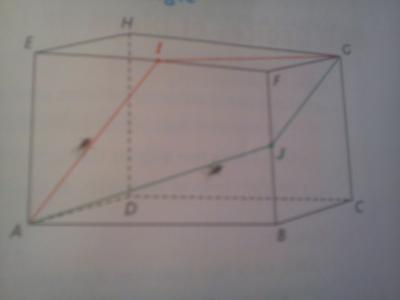
(j'espère que vous pouver voir quelque chose ! )

-
Quelle est la mouche qui effectue le trajet le plus court ?
Ici, j'ai fait les cacluls avec Pythagore, mais je ne sais pas si c'est normal de tomber sur des racine carré ( ou nombres infinis) dans tous les calculs !!?
-
Quel est le trajet le plus court, parmi tous les trajets possibles, pour aller de A à G, en suivant des segments de droites sur les faces ? (Attention, la boite est posée sur le sol ! )
(Indication : Il est peut être utile de réaliser un patron) -
Finalement, les deux mouches décident de se rendre au point G le plus rapidement possible sans s'imposer de contrainte ( elles peuvent voler ! ).
Quelle distance vont-elles parcourir dans ce cas ?
Merci a tous ceux qui me répondront !!

Bonne journée
Cordialement
-
-
AAnonyme dernière édition par
Hello LoloZazaMiss
AC = AJ +JC
et ABJ triangle rectangle, on connait BJ car J milieu de BF
on connait AB, on peut connaitre avec Pythagore AJ
Raisonnement Identique pour CFGidem pour AC = AI + IC
donc tu peux donner le détail de
tes calculs et on verra si tout est OK ...
-
LLiliZazaMiss dernière édition par
Alors...
On sait que I est le milieu de [EF]. donc [EI]= 4 et [IF]= 4
Dans le triangle AEI, rectangle en E, on utilise le théorème de Pythagore.
AI²=4²+4²
AI²=16+16
AI= √32Dans le triangle IFG, rectangle en F, on utilise le théorème de Pythagore :
IG²= IF²+FG²
IG²= 4²+6²
IG²= 16+36
IG= √52AI+IG= √32+√52
(ce qui donne environ 12,86)On sait aussi que J est le milieu de [BF]
donc [BJ]=2 et [JF]=2Dans le triangle ABJ rectangle en B, on utilise le théorème de Pythagore :
AJ²= AB²+IB²
AJ²= 8²+2²
AJ²= 64+4
AJ= √68Dans le triangle JFG, rectangle en F, on utilise le théorème de Pythagore :
JG²= JF²+FG²
JG²= 2²+6²
JG²= 4+36
JG= √40AJ+JG= √68+√40
(ce qui donne environ 14,56)La mouche qui a prit le trajet le plus court est la mouche 1 !
Je pense que c'est assez complet ! J'espère que c'est juste !

-
LLiliZazaMiss dernière édition par
C'est surtout pour les questions d'après que je bloque......
 :frowning2:
:frowning2:
-
AAnonyme dernière édition par
ça me parait Juste !
Pour le 2) tu as une idée ?
-
LLiliZazaMiss dernière édition par
J'aurai pensé AG, mais c'est a l'interieur de la boite... Donc il faut trouver des droites SUR les faces... et c'est la que je bloque !

J'ai réfléchi depuis ce matin, mais je n'ai eu aucune idée..
-
LLiliZazaMiss dernière édition par
Peut-être AF puis FG
-
LLiliZazaMiss dernière édition par
J'ai calculé AF puis FG et le résultat donne 6+√80 ou environ 14,94... ce qui est plus long que les trajets des mouches...
Je ne voit vraiment pas ce que cela pourrait être...
-
AAnonyme dernière édition par
Je pense que l'énoncé
"Indication : Il est peut être utile de réaliser un patron "
est à suivreJe réfléchis de mon coté ...
Il n'est pas interdit aux autres forumeurs de donner
des idées / un avis là-dessus ...
-
LLiliZazaMiss dernière édition par
Merci beaucoup ! ^^
Je vais construire le patron et je vous tient au courant si je trouve quelque chose !
-
AAnonyme dernière édition par
Dessine ton patron à plat sur une feuille
tu prends un rectangle de 8cm * 4cm
au centre de ta feuille
puis accolé au dessus un autre de 8cm * 6 cmEtc ... là tu trouveras vite des idées de réponse

-
LLiliZazaMiss dernière édition par
Ok merci !
-
LLiliZazaMiss dernière édition par
Je n'ai toujours pas trouvé de réponse....
Est-ce que quelqu'un pourrait m'aider SVP ?
Je suis un peu perdue....