Déterminer graphiquement l'ensemble de définition d'une fonction
-
Lloulou08 dernière édition par Hind
Bonjour a tous,
Je bloque avec une question et j'aimerais savoir si le reste est juste
 , alors voici l'énoncé :
, alors voici l'énoncé :Soient aaa un réel fixé et f:⟹ax2−5−2x+1f: \Longrightarrow \frac{ax^2-5}{-2x+1}f:⟹−2x+1ax2−5
- Déterminer l'ensemble de définition de fff.
Voici ma réponse: f(x)=ax2−5−2x+1f(x)=\frac{ax^2-5}{-2x+1}f(x)=−2x+1ax2−5
donc:
−2x+1=0-2x+1=0−2x+1=0
−2x=−1-2x= -1−2x=−1
x=12x=\frac{1}{2}x=21DfDfDf est l'ensemble de tous les réels privé de 12\frac{1}{2}21
Df=R−12Df=\mathbb{R}-{\frac{1}{2}}Df=R−21Est-ce juste

- Déterminer la valeur de aaa sachant que la courbe de fff passe par le point de coordonnées (1; -1)
Là je bloque totalement, si vous pouvez m'apporter de l'aide merci

- Voici le graphique:
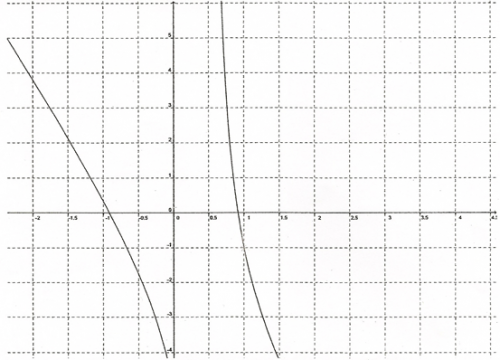
a. Déterminer graphiquement l'ensemble de définition de la fonction x⟹1f(x)x\Longrightarrow \frac{1}{f(x)}x⟹f(x)1
Voici ma réponse : Graphiquement f(x)=0f(x)=0f(x)=0 pour x=−0,9;0,9x= -0,9; 0,9x=−0,9;0,9 donc l'ensemble de définition de la fonction x⟹1f(x)x\Longrightarrow \frac{1}{f(x)}x⟹f(x)1 est R−−0,9;0,9\mathbb{R} - {-0,9; 0,9}R−−0,9;0,9.
Est-ce juste

b. Déterminer graphiquement l'ensemble de définition de la fonction x⟹f(x)x\Longrightarrow \sqrt{f(x)}x⟹f(x).
Voici ma réponse: Graphiquement f(x)≥0f(x)\ge 0f(x)≥0 sur ] -0,9; 0,9] donc l'ensemble de définition de la fonction x⟹f(x)x\Longrightarrow \sqrt{f(x)}x⟹f(x) est ]−∞;−0,9]∪]+∞;0,9]]-\infty;-0,9]\cup ]+\infty; 0,9]]−∞;−0,9]∪]+∞;0,9].
Est-ce juste

Merci de votre réponse.
-
AAnonyme dernière édition par
Hello Loulou08
- Ok
- si f passe par le point de coordonnées (1; -1)
alors f(1) = -1 ...
-
Lloulou08 dernière édition par
Bonjour messinmaisoui,
- f(1)=−1∗12−5−2∗1+1f(1)=\frac{-1* 1^2-5}{-2*1+1}f(1)=−2∗1+1−1∗12−5
donc la valeur de aaa serait -1 ?
Merci
-
AAnonyme dernière édition par
Pas exactement ...
f(1)=a∗12−5−2∗1+1=−1f(1)=\frac{a* 1^2-5}{-2*1+1} = -1f(1)=−2∗1+1a∗12−5=−1
il faut trouver a maintenant
-
Lloulou08 dernière édition par
Je regarde ça
Merci
-
Lloulou08 dernière édition par
f(1)=a<em>12−5−2</em>1+1=−1f(1)=\frac{a<em>1^2-5}{-2</em>1+1}=-1f(1)=−2</em>1+1a<em>12−5=−1
a<em>12−5=−2</em>1+1−1a<em>1^2-5=-2</em>1+1-1a<em>12−5=−2</em>1+1−1
a<em>12−5=−2a<em>1^2-5=-2a<em>12−5=−2
a</em>1−5+2=0a</em>1-5+2=0a</em>1−5+2=0
a∗1−3=0a*1-3 =0a∗1−3=0
a=3a=3a=3Est-ce juste ?
-
AAnonyme dernière édition par
Non
Tu as fait une erreur dans le 2eme ligne ...
Je trouve :
a - 5 = -1
et a = 4
-
Lloulou08 dernière édition par
Je vois pas mon erreur, ça serait le 1 messi ?
Merci
-
AAnonyme dernière édition par
Alors l'erreur est la suivante
à la 2eme ligne
tu as, je schématise ... a / b = -1
et tu fais a = b - 1 au lieu de a = (-1) * b
-
Lloulou08 dernière édition par
Ok merci alors,
f(1)=a<em>12−5−2</em>1+1=−1f(1)=\frac{a<em>1^2-5}{-2</em>1+1}=-1f(1)=−2</em>1+1a<em>12−5=−1
a<em>12−5=(−1)</em>(−2)∗1+1a<em>1^2-5=(-1)</em>(-2)*1+1a<em>12−5=(−1)</em>(−2)∗1+1Mais après quand je fais le calcul ça ne va plus car je trouve a=-2
-
AAnonyme dernière édition par
Je me suis aussi trompé
 donc
donc
voici le résultat correct ...f(1)=a<em>12−5−2</em>1+1=−1f(1)=\frac{a<em>1^2-5}{-2</em>1+1}=-1f(1)=−2</em>1+1a<em>12−5=−1
a−5=(−1)∗(−1)a-5=(-1)*(-1)a−5=(−1)∗(−1)
a−5=1a-5=1a−5=1
a=6a=6a=6
-
Lloulou08 dernière édition par
^^ pas grave ca arrive a tout le monde
f(1)=a<em>12−5−2</em>1+1=−1f(1)=\frac{a<em>1^2-5}{-2</em>1+1}=-1f(1)=−2</em>1+1a<em>12−5=−1
a<em>12−5=(−1)</em>[(−2)<em>1+1]a<em>1^2-5=(-1)</em>[(-2)<em>1+1]a<em>12−5=(−1)</em>[(−2)<em>1+1]
a−5=(−1)</em>(−1)a-5=(-1)</em>(-1)a−5=(−1)</em>(−1)
a−5=1a-5=1a−5=1
a=6a=6a=6J'ai mis l'étape en plus et ca revient au même.
Merci et pour la suite c'est correct messi ?
-
AAnonyme dernière édition par
C'est OK pour a)
Pour b) Je ne suis pas OK
Pour x = 1,5, f(1,5) sera négatif par exemple
et pour x =0,8, f(0,8) sera positif ...
-
Lloulou08 dernière édition par
b)Graphiquement f(x)≥0f(x)\ge 0f(x)≥0 sur ] -0,9; 0,9] donc l'ensemble de définition de la fonction x⟹f(x)x\Longrightarrow \sqrt{f(x)}x⟹f(x) est ]-0,9;0.9].
Ça serait comme ça ?
-
AAnonyme dernière édition par
Non ...
il faut prendre f(x) > 0 soit y > 0
ou les ordonnées positives
donc je dirais
=>
]-OO,-0,9] U ] x; 0,9]avec x = 0,5 je pense, bien regarder le grahique ...
-
Lloulou08 dernière édition par
Ok merci beaucoup messi de ton aide.
Bonne soirée.