Devoir de mathématiques sur les identités remarquables
-
Eendymion dernière édition par
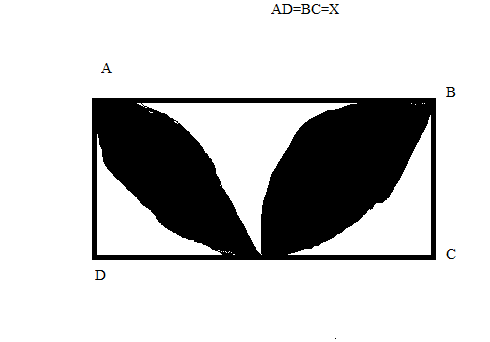
Bonjour, j'ai un DM de maths pour la rentrée et je dois exprimer l'aire des parties en noir en fonction de X :
(voir image)
Vu que [AD] est le diamètre du cercle de gauche, je pensais calculer l'aire du cercle avec pi.
Quelqu'un aurait-il une piste ??
Merci d’avance.
PS : la figure n'est pas très bien faite (faite sur Paint)
-
Bonsoir endymion,
Calcule l'aire d'un quart de cercle et soustrais l'aire du triangle.
Tu obtiens ainsi 1/4 de l'aire noire.
-
Eendymion dernière édition par
Bonjour, je soustrais l'aire de quel triangle ?
-
Je suppose que DC = 2 AD.
Soit M le milieu du segment [DC],
Tu soustrais l'aire du triangle ADM.
-
Eendymion dernière édition par
Donc je fais :
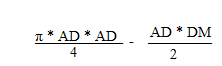
??
-
Oui,
mais la tu as 1/4 de l'aire de la partie noire.
Remplace les mesures des cotés en fonction de x.
-
Eendymion dernière édition par
D'accord, donc je multiplie le tout par 4 ??
-
Oui, la figure admet un axe de symétrie.
-
Eendymion dernière édition par
D'accord, mais je suis bloqué après :
Je me retrouve avec (πx² - 2x² /4 ) * 4 et je ne peux plus après.
-
Simplifie l'expression.
-
Eendymion dernière édition par
Euh.. Si on divise quelque chose par 4, puis on le multiplie par 4, ça revient à garder l'expression d'origine ?Non ?
Donc j'obtiens πx² - 2x² au final ??
-
oui,
C'est correct.
-
Eendymion dernière édition par
Après je ne voie pas comment réduire plus.
Je pense que c'est terminé.
-
Oui,
C'est le résultat.