DM - Fonctions

Bonjour,

Je dois faire donc un DM, mais je bloque a partir la question 3.
Voila déjà le sujet, puis après les réponses (que j'ai trouvé) pour la 1 et la 2.

Figure:

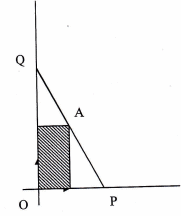
Soit le rectangle colorié (voir figure), dont le quatrième sommet est le point A de coordonnées (1;2).
Le point P a pour coordonnées (x;0) avec x>1.
Q est l'intersection de la droite (AP) avec l'axe des ordonnées.
On appelle L(x) la distance OQ et A(x) l'aire du triangle OPQ.

Questions:

Exprimer L(x) et A(x) en fonction de x.
Remplir ce tableau de valeurs approchées pour ces deux fonctions:
1.1 | 1.5 | 2 | 2.5 | 3 | 4 | 5 | 6
L(x)
A(x)

Quelles conjectures peut-on faire quant aux variations de L et de A ?

Etudier, par le calcul, les variations de la fonction L, puis l'existence éventuelle de maximum et minimum pour L.
Déterminer le signe de A(x) - A(2). Que vient-on de prouver pour A?
Montrer que, pour a et b éléments de ]1;+infini[, on obtient:

A(a) - A(b) =
(a-b)[(a-1)(b-1)-1]
(a-1)(b-1)

Montrer que, si a < b, A(a)-A(b) a un certain signe sur l'intervalle ]1;2] et un autre signe sur l'intervalle [2;+infini[. Que vient-on de prouver pour A ?

(j'ai fait une image pour faire les fractions et le tableau)

Après pour la suite je bloque..
Rappel de la question 3:
Etudier par le calcul les variations de la fonction L puis l’existence éventuelle de maximum et minimum pour L.

L(x) = (2(x-1)+2))/(x-1)=2+2/(x-1) donc L(x) strictement décroissante sur le domaine étudié de +infini à 2 (minimum)
A(x)-A(2)= 4x²/(x-1) -16 = (x²-4x+4)×4/(x-1)= (x-2)²×4/(x-1) donc toujours positif dans le domaine étudié, donc A(x) toujours strictement supérieur à 2 (minimum)
A(x) est décroissante puis croissante, son minimum est en x=2 et A(2) = 16